Поняття математичної структури, аксіоматичної теорії математичної структури, ізоморфізму математичних структур. Поняття моделі (інтерпретації) системи аксіом.

Математичною структурою називається сукупність елементів одного або кількох множин, відношень, які задані між цими елементами, та аксіом, яким задовольняють ці відношення. Будемо позначати

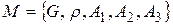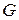Приклад. Математична структура групи має вигляд , де - будь-яка непуста множина, 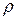- алгебраїчна операція 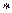на ,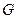

,

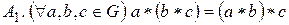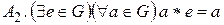, елемент називають нейтральним елементом,

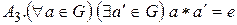, елемент 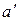називають симетричним до 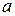елементом.

Аксіоматичною теорією даної математичної структури називається сукупність тверджень, які можна вивести із системи аксіом цієї структури, користуючись лише правилами логіки.

Для однієї математичної структури можна будувати різні аксіоматичні теорії. Вони можуть відрізнятись списками аксіом, теорем, означень. Геометрію, наприклад евклідову, можна викласти аксіоматичним методом, базуючись на різних системах аксіом.

Моделлю (або інтерпретацією) системи аксіом називаються множини елементів конкретної природи, на яких означені всі відношення та виконані всі аксіоми даної структури.

Приклад.Модель структури групи.

Нехай 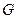є множиною 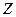цілих чисел, 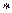- додавання цілих чисел. Ця алгебраїчна операція є асоціативною, 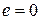, для кожного цілого числа маємо .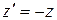

Дві математичні структури (або їх моделі) називаються ізоморфними, якщо між елементами множин та відношеннями встановлена бієкція так, що елементам однієї структури (моделі), які знаходяться у деякому відношенні, відповідають елементи другої структури (моделі), які знаходяться у відповідному відношенні.

Аксіоматичним методом теорія будується формально, без опори на інтуїцію, очевидність і т. ін., але один раз побудована теорія може бути реалізована на різних множинах об’єктів – на різних інтерпретаціях.