Вимоги до системи аксіом.

1. Несуперечливість (сумісність).

2. Незалежність (мінімальність).

3. Повнота (достатність).

Означення. Система аксіом називається внутрішньо несуперечливою, якщо з неї не можна вивести 2 протилежних твердження: 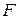і .

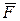Система аксіом називається змістовно несуперечливою, якщо існує хоча б одна її модель. Отже, питання про змістовну несуперечливість системи аксіом зводиться до питання несуперечливості її моделі.

Означення. Говорять, що аксіома 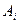в системі аксіом 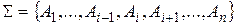є незалежною, якщо вона не є наслідком інших аксіом цієї системи. Система аксіом називається незалежною, якщо в ній кожна аксіома незалежна.

Теорема. Нехай задано систему аксіом 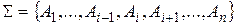. Розглянемо нову систему аксіом 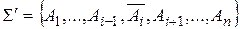. Якщо система аксіом 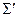несуперечлива, то аксіома 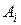в системі аксіом 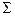є незалежною.

Доведення.Застосуємо метод від супротивного. Припустимо, що аксіома 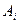в системі 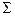є залежною, тобто в аксіоматичній теорії, побудованій на базі системи аксіом 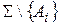, твердження 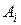є теоремою. Але тоді в аксіоматичній теорії, побудованій на базі системи аксіом 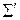, справедливі твердження 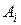(теорема) і 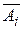(аксіома), отже система аксіом 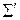суперечлива. Теорема доведена.

Означення. Система аксіом називається повною, якщо її не можна доповнити твердженням, яке б:

1. не суперечило аксіомам системи,

2. не залежало від них,

3. не вводило нових неозначуваних понять.

Теорема. Якщо будь-які дві моделі даної системи аксіом ізоморфні, то вона повна.

Доведення.Нехай система аксіом 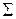є неповною. За означенням існує твердження 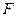таке, що не містить нових неозначуваних понять, система 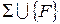є несуперечливою і твердження 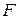в ній є незалежним. Розглянемо моделі систем аксіом 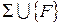і 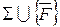. Вони є також моделями системи аксіом 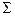, причому не ізоморфними, адже в одній моделі виконується 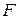, а в іншій 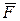. Теорема доведена.