Раціональне число–це клас попарно рівних між собою впорядкованих пар.

Теорема.Додавання раціональних чисел комутативне і асоціативне.

Теорема.Множення раціональних чисел комутативне, асоціативне і дистрибутивне по відношенню до додавання.

Доведення легко проводиться на мові пар.

Означення.Різницею раціонального числа 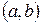і раціонального числа називається таке раціональне число , що .

Теорема.Різниця раціональних чисел завжди існує і єдина.

Доведеннявипливає з формули

,

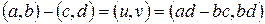яку легко отримати, використовуючи означення різниці.

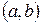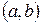Означення.Часткою від ділення раціонального числа на раціональне число називається таке раціональне число , що . При цьому число називається діленим, а число – дільником.

Теорема.Частка двох раціональних чисел завжди існує і єдина, якщо перша компонента дільника не дорівнює 0.

Доведеннявипливає з формули

,

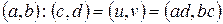яку легко отримати, використовуючи означення різниці.

Покажемо , що множина раціональних чисел є мінімальним розширенням множини цілих чисел. Розглянемо раціональні числа, друга компонента яких дорівнює 1, тобто множину . Легко отримати співвідношення:

,

,

.

,

.

,

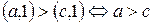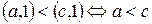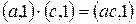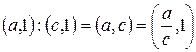, якщо ціле число 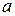ділиться на ціле число .

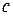Тобто, якщо ввести взаємно однозначну відповідність за правилом , то для неї виконуються вимоги ізоморфізму. Ми отримали, що множина М ізоморфна множині 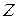, або, інакше, що множина 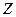є підмножиною множини 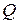. А це, в свою чергу, означає, що 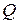є розширенням множини 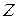і важливо відмітити, що в цьому розширенні операція ділення чисел завжди виконується.

В силу введеної відповідності рівність 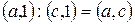можна переписати у вигляді

,

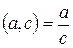який будемо називати другою формою запису раціонального числа. Отже, раціональне число – це частка двох цілих чисел при умові, що друге число не дорівнює нулю.

Означення.Будь-яке раціональне число, менше за число , називається від’ємним.

За аксіомою 1.2) отримаємо 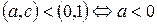, тобто від’ємним є раціональне число, в якому компоненти мають різні знаки. Розділивши обидві компоненти від’ємного раціонального числа на його другу компоненту, отримаємо

, .

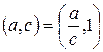Далі можна доводити властивості нерівностей, ввести дії над нерівностями. Наведемо, для прикладу одну з цих теорем.

Теорема.При множенні обох частин вірної нерівності 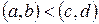на від’ємне раціональне число 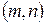отримується вірна нерівність

.

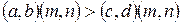Доведення.За умовою 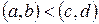, тобто за аксіомою 1.2) , . Число 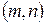від’ємне, значить . Помножимо обидві частини нерівності на від’ємне ціле число 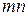. За властивостями нерівностей для цілих чисел отримаємо , з якої за аксіомою 1.1) можемо записати , а за аксіомою 3) отримаємо нерівність

,

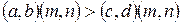яку і треба було довести.