аргументу. Число е.
Перша “чудова” границя та її наслідки.
Розглянемо функцію 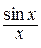 . Вона невизначена при х=0: чисельник і знаменник дорівнюють нулю. Знайдемо границю цієї функції при
. Вона невизначена при х=0: чисельник і знаменник дорівнюють нулю. Знайдемо границю цієї функції при 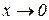 .
.
Візьмемо коло одиничного радіуса (рис. 3.1). Його центральний кут МОА позначимо через х , причому 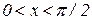 . Безпосередньо з рисунка випливає, що
. Безпосередньо з рисунка випливає, що
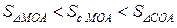 , (4.1)
, (4.1)
де 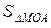 ,
, 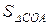 ,
, 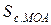 – площа відповідно трикутників МОА, СОА, і сектора МОА. Знайдемо вказані площі:
– площа відповідно трикутників МОА, СОА, і сектора МОА. Знайдемо вказані площі:
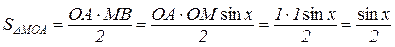 ,
,
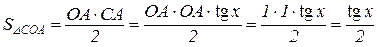 ,
,
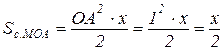 .
.
Тепер нерівність (4.1) набирає вигляду:
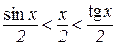 .
.
Помноживши всі члени останньої нерівності на 2/sinx отримаємо:
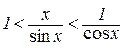
або
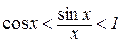 . (4.2)
. (4.2)
Нерівність (4.2) отримано за умови, що x>0, але
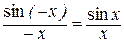 і
і 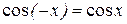 ,
,
тому вона справедлива й при x<0.
Оскільки
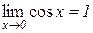 і
і 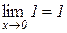 ,
,
то з теореми 3.9 випливає, що
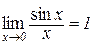 . (4.3)
. (4.3)
Означення 4.1.Рівність (4.3) будемо називати першою “чудовою” границею.
Наведемо основні наслідки першої “чудової” границі.
Наслідок 4.1.1. 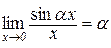 , де
, де 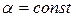 .
.
Дійсно,
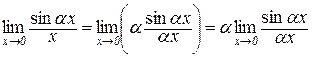 .
.
Зробимо заміну αx=z, тоді 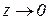 при
при 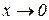 і останній вираз дає
і останній вираз дає
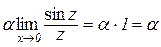
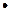
Наслідок 4.1.2. 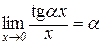 .
.
Дійсно,
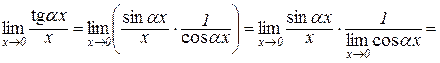
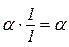
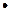
Наслідок 4.1.3. 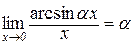 .
.
Дійсно, зробимо заміну 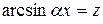 , тоді
, тоді 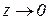 при
при 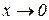 і
і 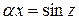 . Таким чином,
. Таким чином,
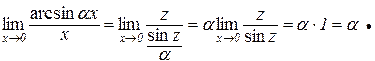
Наслідок 4.1.4. 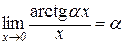 .
.
Справедливість цієї рівності доводиться аналогічно попередньому наслідку 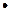
2.2. Друга “чудова” границя для дискретного
аргументу. Число е.
Розглянемо змінну величину
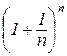 , (4.4)
, (4.4)
де n набуває цілих додатних значень.
Теорема 4.1. Змінна величина (4.4) при 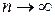 має границю, яка належить проміжку (2; 3).
має границю, яка належить проміжку (2; 3).
Доведення. Використаємо для (4.4) формулу бінома Ньютона:
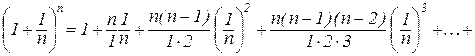
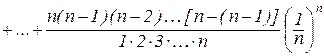 . (4.5)
. (4.5)
Зробимо в (4.5) нескладні алгебраїчні перетворення:
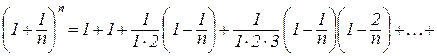
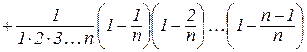 . (4.6)
. (4.6)
З (4.6) випливає, що змінна величина (4.4) зростає при зростанні n. Справді, при переході від n до n+1 кожний доданок правої частини (4.6) зростає:
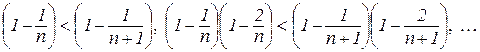
і добавляється ще один (n+2)-й доданок. Усі члени розкладу (4.6) додатні.
Покажемо, що змінна величина (4.4) обмежена.
Дійсно,
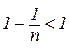 ,
, 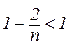 , ... ,
, ... ,
тому з (4.6) маємо
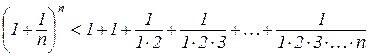 . (4.7)
. (4.7)
Зауважимо, що
 ,
,
тому (4.7) можна записати у вигляді
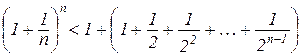 .
.
Сума в дужках утворює геометричну прогресію із знаменником q=1/2 і першим членом рівним 1, тому
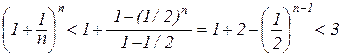 . (4.8)
. (4.8)
Таким чином, з (4.6) і (4.8) отримуємо
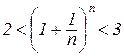 . (4.9)
. (4.9)
З теоремою 3.12 слідує, що змінна величина (4.4) має границю.
Означення 4.2. Границя змінної величини 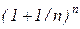 при
при 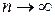 називається числом е, тобто
називається числом е, тобто
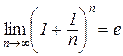 . (4.10)
. (4.10)
З (4.9) і теоремою 3.12 маємо 2<e<3. Теорему доведено 
Означення 4.3. Границю (4.10) в подальшому будемо називати другою “чудовою” границею.
Наведемо значення числа е з точністю до перших десяти знаків після коми: е=2,7182818284…
4.3. Друга “чудова” границя для неперервного
Аргументу.
Теорема 4.2. Функція 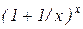 прямує до числа е при
прямує до числа е при 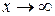 , тобто
, тобто
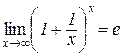 . (4.11)
. (4.11)
Доведення. Використаємо рівність (4.10), де n приймає цілі додатні значення. Змінна ж х може приймати як дробові так і від’ємні значення. Розглянемо окремо випадки 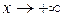 і
і 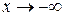 .
.
а) Нехай 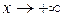 . Для кожного значення х можна знайти ціле число n таке, що
. Для кожного значення х можна знайти ціле число n таке, що
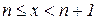 або
або 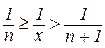 .
.
Зробимо нескладні перетворення останньої нерівності
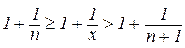
і
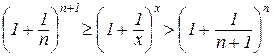 . (4.12)
. (4.12)
Очевидно, що 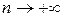 при
при 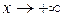 . Знайдемо в (4.12) границю змінних величин при
. Знайдемо в (4.12) границю змінних величин при 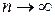 :
:
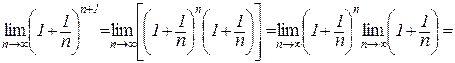
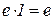 ,
,
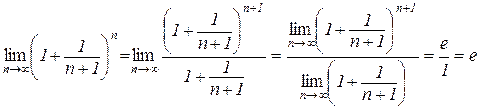 .
.
Таким чином, з теореми 3.9 випливає, що
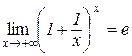 .
.
б) Нехай 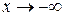 . Введемо нову змінну
. Введемо нову змінну
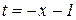 або
або 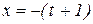 .
.
Тоді, враховуючи, що 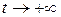 при
при 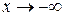 , отримаємо:
, отримаємо:
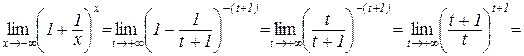
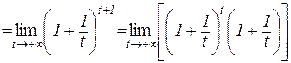
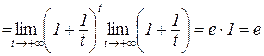 .
.
Таким чином, теорему доведено 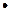
Границю (4.11) ще називають другою “чудовою” границею для неперервного аргумента.
Приклад 4.1. Знайти
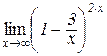 .
.
Розв’язування. Зробимо заміну 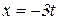 , тоді
, тоді 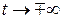 при
при 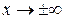 і
і
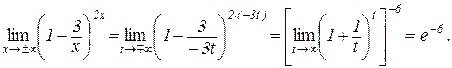
Приклад. 4.2. Знайти
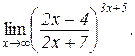
Розв’язування. Зробимо тотожні перетворення:
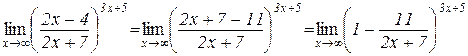
Введемо нову змінну
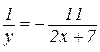 або
або 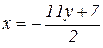 ,
,
тоді 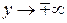 при
при 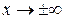 і остання границя прийме вигляд:
і остання границя прийме вигляд:
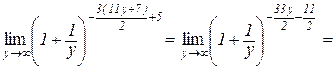
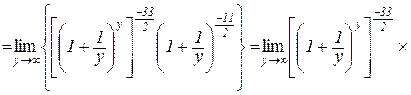
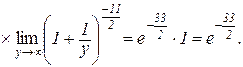
Означення 4.3. Логарифм 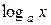 , основа якого дорівнює числу е, називається натуральнимлогарифмом і позначається
, основа якого дорівнює числу е, називається натуральнимлогарифмом і позначається 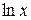 , тобто
, тобто
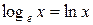 .
.
Розглянемо два основні наслідки границі (4.11):
Наслідок 4.2.1.
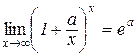 . (4.13)
. (4.13)
Дійсно, зробимо в (4.11) заміну x/a=z, тоді 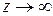 при
при 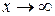 і x=za. Отримаємо:
і x=za. Отримаємо:
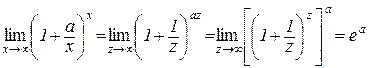
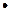
Наслідок 4.2.2.
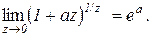 (4.14)
(4.14)
Дійсно, зробимо в (4.11) заміну z=1/x, тоді 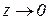 при
при 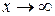 і x=1/z. Отримаємо:
і x=1/z. Отримаємо: 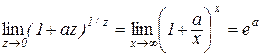
Запитання для самоконтролю.
1. Що таке перша “чудова” границя?
2. Які ви знаєте наслідки з першої “чудової” границі?
3. Сформулюйте і доведіть теорему про границю 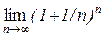 .
.
4. Що таке число е?
5. Чому рівна границя функції 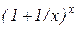 при
при 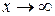 ?
?
6. Що означає запис 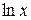 ?
?
7. Які ви знаєте наслідки другої “чудової” границі?
Приклади до розділу 4.
1. Знайти границі:
а) 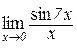 . .
| Відп.: 7; | б) 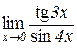 . .
| Відп.: 3/4; |
в) 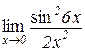 . .
| Відп.: 18; | г) 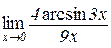 . .
| Відп.: 4/3; |
д) 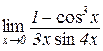 . .
| Відп.: 1/8; | е) 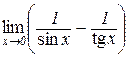 . .
| Відп.: 0; |
є) 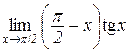 . .
| Відп.: 1; | ж) 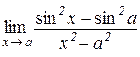 . .
| Відп.: 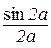 ; ;
|
з) 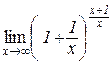 . .
| Відп.: 1; | и) 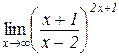 . .
| Відп.: 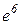 ; ;
|
і) 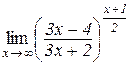 . .
| Відп.: 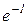 ; ;
| ї) 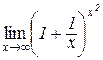 . .
| Відп.: 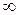 . .
|
| <== предыдущая лекция | | | следующая лекция ==> |
| основні властивості. | | | Неперервність функції в точці. |
Дата добавления: 2016-05-05; просмотров: 1375;
