основні властивості.

Поняття нескінченно малих величин та їх

Означення 3.1. Функція 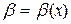називається нескінченно малою при 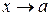( 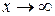), якщо

( ).

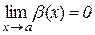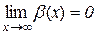Приклад 3.1. Функція 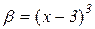є нескінченно малою при 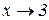тому, що

.

Приклад 3.2. Функція β=3/(x+7) є нескінченно малою при 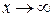, оскільки

.

Розглянемо основні властивості нескінченно малих.

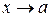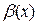Теорема 3.1. Для того щоб функцію y=f(x) можна було подати у вигляді суми сталої b і нескінченно малої при ( ) функції , тобто 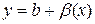, необхідно і достатньо, щоб виконувалась умова

.

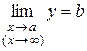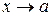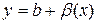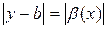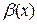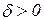Доведення. Необхідність. Для визначеності розглянемо випадок . З рівності випливає, що . Але – нескінченно мала, тому для довільного знайдеться число таке, що для всіх х , які задовольняють умову , виконуватиметься нерівність 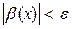і, очевидно, нерівність 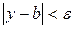. Це означає, що

.

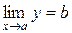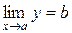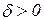Достатність. Якщо , то для довільного найдеться число таке, що для всіх х , які задовольняють умову , виконуватиметься нерівність 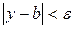. Але, якщо позначити 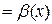, то одночасно виконуватиметься і нерівність 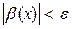, а це означає, що α є нескінченно малою. І, таким чином,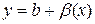

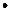
Приклад 2.3. Нехай задана функція y=5+x³. Тоді 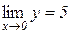, тому що х³ нескінченно мала при 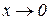. І навпаки, якщо 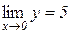, то змінну y можна подати у вигляді суми числа 5 і нескінченно малої функції β(х) при 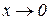, наприклад, х³.

Теорема 3.2. Якщо нескінченно мала функція при 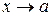( 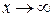), то функція y=1/β(х) є нескінченно великою.

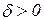Доведення. Якщо β(x) нескінченно мала, то для довільного як завгодно малого числа знайдеться число таке, що для всіх х, які задовольняють умову , виконуватиметься нерівність

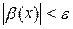або .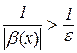

Отже, для як завгодно великого числа 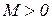можна знайти число ε таке, що 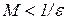. А це означає, що функція 1/β(x) є нескінченно великою

Теорема 3.3. Алгебраїчна сума скінченої кількості нескінчено малих функцій є нескінченно малою функцією.

Доведення. Доведення проведемо для двох доданків, оскільки для довільної кількості доданків воно аналогічне.

Нехай u(x)=β₁(х)+β₂(х), де β₁(х) і β₂(х) нескінченно малі при 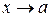. Покажемо, що для довільного як завгодно малого ε>0 знайдеться число δ>0 таке, що з виконання умови випливатиме справедливість нерівність 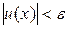. Дійсно, оскільки β₁(х) і β₂(х) нескінченно малі, то для вказаного ε знайдуться числа δ₁>0 і δ₂>0 такі, що при виконанні умов 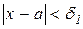і 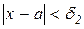справджуватимуться нерівності, відповідно,

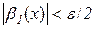і . (3.1)

В якості δ візьмемо менше з чисел δ₁, δ₂. Тоді для всіх х, які задовольняють умову , виконуватимуться одночасно обидві нерівності (3.1). Таким чином, в околі 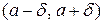матимемо

.

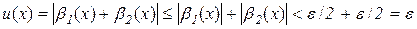Аналогічно проводиться доведення у випадку

Теорема 3.4. Добуток нескінченно малої функції β=β(х) на обмежену функцію z=z(x) при 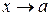( 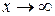) є нескінченно малою функцією при ( ).

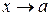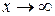Доведення. Розглянемо випадок 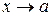. З означення обмеженої функції випливає, що існує число М>0 і окіл 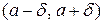точки а, в якому виконується нерівність , а з означення нескінченно малої слідує, що для довільного як завгодно малого ε>0 знайдеться окіл , в якому виконується нерівність 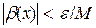. Для меншого із вказаних околів матимемо

.

А це означає, що β(х)/z(x) – нескінченно мала.

Для випадку 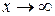доведення проводиться аналогічно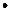

Наслідок 3.4.1. Добуток двох нескінченно малих функцій є нескінченно мала функція.

Це слідує з того, що нескінчено мала функція є обмеженою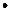

Наслідок 3.4.2. Добуток нескінченно малої функції на сталу є нескінченно малою функцією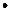

Теорема 3.5. Відношення β(х)/z(x), де β(х) нескінченно мала, а границя функції z(x) відмінна від нуля, є нескінченно малою функцією.

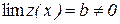Доведення. Нехай і . За теоремою 2.2 функція 1/z(x) обмежена. Отже, ми отримали добуток нескінченно малої на обмежену функцію, який за теоремою 3.4 є нескінченно малою функцією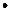

3.2. Основні теореми про границі.

Нижче розглянуто границі функцій аргументу х при 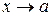( 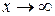). Для простоти викладок запис 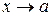( 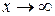) в подальшому будемо опускати.

Теорема 3.6. Границя алгебраїчної суми скінченої кількості функцій дорівнює алгебраїчній сумі границь цих функцій, тобто

.

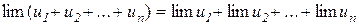Доведення. Доведення проведемо для двох доданків. Нехай

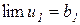, і limu₂=b₂ .

Тоді за теоремою 3.1 можна записати

u₁=b₁+β₁ , і u₂=b₂+β₂ ,

де β₁ і β₂ – нескінченно малі. Таким чином,

u₁+u₂=(b₁+b₂)+(β₁+β₂).

Оскільки сума b₁+b₂ є сталою величиною і за теоремою 3.3 величина β₁+β₂ є нескінченно малою, то за теоремою 3.1 отримуємо:

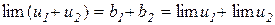
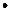
Приклад 3.4.

.

Теорема 3.7. Границя добутку скінченої кількості функцій дорівнює добутку границь кожної з цих функцій.

Доведення. Доведення проведемо для двох множників. Нехай limu₁=b₁ і limu₂=b₂. Тоді з теореми 3.1 маємо u₁=b₁+β₁ і u₂=b₂+β₂, де β₁, β₂ – нескінченно малі, і, отже,

.

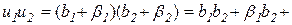
Тут b₁b₂ – стала, b₁β₂+β₂b₁+β₁β₂ – нескінченно мала величина за теоремами 3.3 і 3.4.

Значить, з теореми 3.1 отримуємо

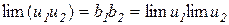
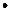
Наслідок 3.7. Постійний множник можна виносити за знак границі.

Дійсно, якщо lim u₁=b₁ і с – стала величина, то

lim(u₁ c)=limu₁ limc=c limu₁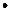

Приклад 3.5.

.

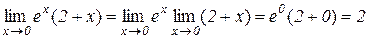Теорема 3.8. Границя відношення двох функцій дорівнює відношенню границь цих функцій, якщо границя знаменника відмінна від нуля, тобто

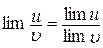, якщо .

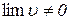Доведення. Нехай limu=b, , тоді u=b+β і 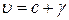, де β і γ – нескінченно малі. Зробимо тотожні перетворення:

.

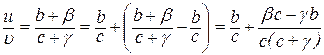Перший доданок останньої суми є стала величина, а другий за теоремою 3.5 – нескінчено мала величина, оскільки чисельник 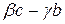є нескінченно малим (див. теоремами 3.3 і 3.4), а границя c(c+γ) рівна . Отже, з теоремою 3.1 випливає, що

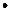
Приклад 3.6. Знайти границю

.

Розв’язування: Так як

,

то за теоремою 3.8

.

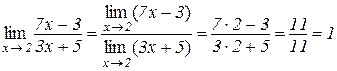Приклад 7. Знайти границю

.

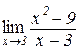Розв’язування. При чисельник і знаменник даного дробу прямують до нуля і, отже, теоремою 3.8 застосовувати не можна. Зробимо тотожні перетворення

,

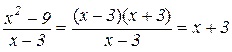які справедливі для всіх значень 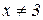. Таким чином, з означення границі функції випливає

.

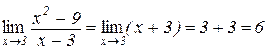Теорема 3.9. Якщо відповідні значення трьох функцій u=u(x), 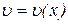, z=z(x) задовольняють умови:

а) ;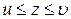

б) ,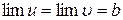

то

.

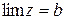Доведення. З умови а) слідує справедливість нерівності

, (3.3)

а з умови б) слідує, що для довільного як завгодно малого ε>0 знайдуться околи і 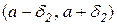, в яких виконуються нерівності відповідно 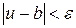і 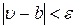. У меншому з околів матимемо

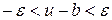і 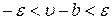. (3.4)

З (3.3) і (3.4) отримаємо 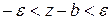, тобто

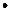
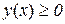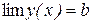Теорема 3.10. Якщо і , то .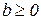

Доведення. Припустимо від супротивного, що b<0. Тоді за умовою теореми 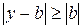, тобто модуль різниці 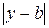більший за додатне число 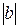і, значить, не прямує до нуля. Але тоді y не прямує до b, що суперечить умові теореми. Таким чином припущення, що b<0 є не правильне. Отже,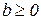

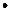
Аналогічно доводиться, що при .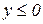

Теорема 3.11. Якщо відповідні значення двох функцій u=u(x) і v=v(x) задовольняють умову 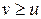, то 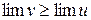, якщо останні існують.

Доведення. З умови теореми виходить, що , тому за теоремою 3.10 або 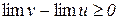. Тобто

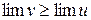
Приклад 3.8. Покажемо, що

.

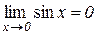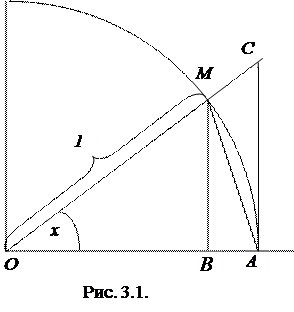З рис. 3.1 випливає, що 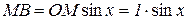, . Тому 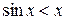, так як 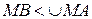. Очевидно, що при x<0 буде 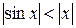. Таким чином з теорем 3.10 і 3.11 дістаємо

,

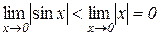тобто початкова рівність доведена.

Приклад 3.9. Покажемо, що

.

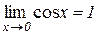Дійсно, , тому

= .

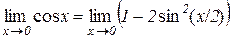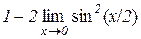Якщо зробити заміну t=x/2, то 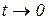при . Таким чином,

.

Сформулюємо без доведення ще одну важливу теорему.

Теорема 3.12. Якщо функція 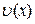є

а) зростаючою;

б) обмеженою, тобто ,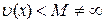

то вона має скінчену границю, тобто

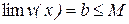
Аналогічна теорема має місце для спадної функції.

Запитання для самоконтролю.

1. Дайте означення нескінченно малої величини.

2. Сформулюйте і доведіть теорему про подання функції у вигляді суми числа і нескінченно малої.

3. Якою величиною є функція, обернена до нескінченно малої?

4. Чому рівна сума нескінченно малих?

5. Чому дорівнює добуток нескінченно малої та обмеженої функцій?

6. Сформулюйте теорему про відношення нескінченно малої та функції відмінної від нуля.

7. Які основні властивості границь ви знаєте?

8. Чому дорівнює границя невід’ємної функції?

9. Сформулюйте теорему про границю монотонної обмеженої функції.

Приклади до розділу 3.

1. Функція u_n набуває значень

.

Показати, що u_n є нескінченно малою при .

2. Показати, що при функція 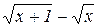є нескінченно малою.