Границя числової послідовності.
Наведемо кілька прикладів змінної величини xn або числової послідовності:
Приклад 2.1.
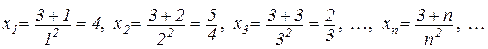
Приклад 2.2.
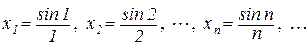
Означення 2.1. Число а називається границею числової послідовності xn , якщо для будь-якого наперед заданого як завгодно малого додатного числа 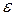 існує номер N такий, що для всіх n>N виконується нерівність
існує номер N такий, що для всіх n>N виконується нерівність 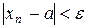 .
.
Якщо число а є границею змінної величини xn , то кажуть, що xn прямує до границі а, і записують 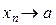 при
при 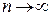 або
або
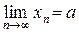 .
.
Приклад 2.3. Покажемо, що змінна величина
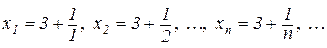
має границю, яка дорівнює 3.
Дійсно,
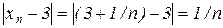 ,
,
і для будь-якого ε можна вказати номер N=[1/ε] такий, що для всіх наступних n>N виконуватиметься нерівність
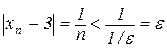 .
.
Отже, 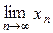 =3.
=3.
Зауваження 2.1. З означення 2.1 випливає, що змінна величина не може мати двох границь. Справді, якщо 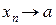 і
і 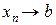 при
при 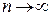 , де для визначеності
, де для визначеності 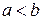 , то
, то 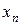 має задовольняти одночасно дві нерівності
має задовольняти одночасно дві нерівності
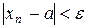 і
і 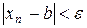 ,
,
для довільних ε. Але це неможливо при ε=(b-a)/2, тому що тоді
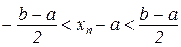 і
і 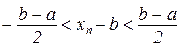
або
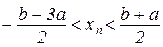 і
і 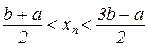 .
.
З останніх двох нерівностей отримуємо, що 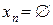 , де
, де 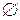 – пуста множина.
– пуста множина.
Зауваження 2.2. Не кожна змінна величина має границю. Наприклад? числова послідовність
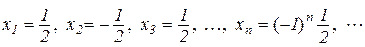
не прямує до певного числа при 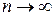 .
.
2.2.Нескінчено великі змінні величини.
Означення 2.2. Змінна величина xn прямує до нескінченності або є нескінченно великою, якщо для будь-якого як завгодно великого додатного числа M можна знайти номер N такий, що для всіх номерів n, які задовольняють умову n>N, виконується нерівність 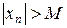 .
.
Приклад 2.4. Змінна величина xn , яка приймає значення
x1=2, x2=1+22, x3=1+32,..., xn=1+n2,...,
є нескінченно великою, оскільки для будь-якого числа M можна вказати номер n= 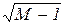 , починаючи з якого всі значення xn задовольняють умову xn>M.
, починаючи з якого всі значення xn задовольняють умову xn>M.
Кажуть, що змінна величина xn прямує до “плюс нескінченності” і записують xn 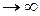 , якщо вона є нескінченно великою і набуває додатних значень.
, якщо вона є нескінченно великою і набуває додатних значень.
2.3. Границя функції.
Розглянемо функцію 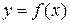 , визначену в околі точки а, за виключенням, можливо, деяких точок цього околу.
, визначену в околі точки а, за виключенням, можливо, деяких точок цього околу.
Означення 2.3. Функція 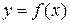 прямує до границі b при прямуванні х до а, якщо для будь-якого як завгодно малого додатного числа ε можна знайти додатне число
прямує до границі b при прямуванні х до а, якщо для будь-якого як завгодно малого додатного числа ε можна знайти додатне число 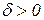 таке, що для всіх х, які задовольняють умову
таке, що для всіх х, які задовольняють умову 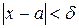 , виконується нерівність
, виконується нерівність
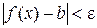 .
.
Якщо b є границею функції 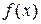 при х
при х 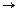 a, то записують
a, то записують
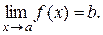
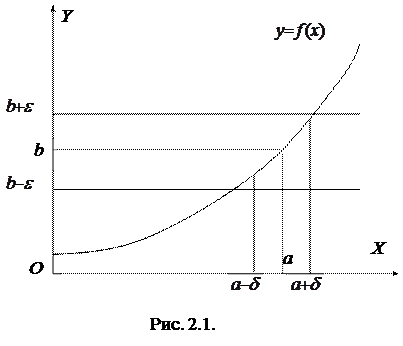 Дамо графічну ілюстрацію поняття границі функції. Якщо з нерівності
Дамо графічну ілюстрацію поняття границі функції. Якщо з нерівності 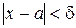 випливає нерівність
випливає нерівність 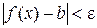 , то це означає, що для всіх точок х з околу (а-δ, а+δ)точки графіка
, то це означає, що для всіх точок х з околу (а-δ, а+δ)точки графіка 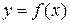 лежать у смузі (b–ε, b+ε) (рис. 2.1).
лежать у смузі (b–ε, b+ε) (рис. 2.1).
Означення 2.4. Якщо функція 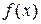 прямує до границі b1 при x
прямує до границі b1 при x 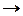 a і x<a, то записують
a і x<a, то записують
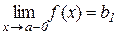 або
або 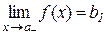
і b1 називають границею функції 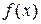 в точці a ліворуч або лівосторонньою границею.
в точці a ліворуч або лівосторонньою границею.
Означення 2.5. Якщо 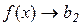 при
при 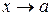 і x>a, то b2 називають границеюфункції
і x>a, то b2 називають границеюфункції 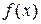 в точці а праворуч або правосторонньоюграницею і записують
в точці а праворуч або правосторонньоюграницею і записують
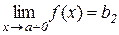 або
або 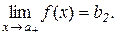
Можна показати: що необхідною і достатньою умовою існування границі функції в точці є існування і рівність лівосторонньої і правосторонньої границь функції в даній точці.
Приклад 2.5. Покажемо, що
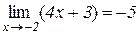 .
.
Дійсно, нехай дано довільне число ε >0. Нерівність
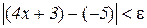
виконуватиметься за умови 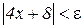 . Отже, при довільному ε для всіх значень х, які задовольняють нерівність
. Отже, при довільному ε для всіх значень х, які задовольняють нерівність 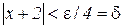 , значення функції 4x+3 відрізнятиметься від –5 менше ніж на ε. Це означає, що –5 є границею нашої функції при х
, значення функції 4x+3 відрізнятиметься від –5 менше ніж на ε. Це означає, що –5 є границею нашої функції при х 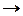 –2.
–2.
Зауваження 2.3. Для існування границі функції при 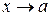 не вимагається, щоб функція була визначена в самій точці
не вимагається, щоб функція була визначена в самій точці 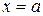 . Знаходячи границю, розглядають значення функції в точках околу а, відмінних від а. Проілюструємо це на прикладі.
. Знаходячи границю, розглядають значення функції в точках околу а, відмінних від а. Проілюструємо це на прикладі.
Приклад 2.6. Покажемо, що
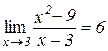 .
.
Розв’язування. Функція
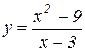 (2.1)
(2.1)
не визначена при x=3. Треба показати, що для довільного ε знайдеться таке δ, що нерівність
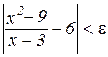 (2.2)
(2.2)
виконуватиметься при 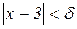 . Але для всіх
. Але для всіх 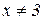 маємо
маємо
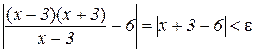
і нерівність (2.2) еквівалентна нерівності
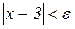 . (2.3)
. (2.3)
Отже при довільному ε нерівність (2.2) буде мати місце, якщо виконуватиметься умова (2.2) (ε=δ). А це означає, що функція (2.1) має границю при 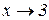 рівну 6.
рівну 6.
Розглянемо деякі випадки поведінки функції при 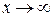 .
.
Означення 2.6. Функція 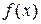 прямує до границі b при
прямує до границі b при 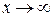 , якщо для кожного як завгодно малого додатного числа ε можна знайти додатне число N таке, що для всіх значень х, які задовольняють умову
, якщо для кожного як завгодно малого додатного числа ε можна знайти додатне число N таке, що для всіх значень х, які задовольняють умову 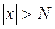 , справджуватиметься нерівність
, справджуватиметься нерівність
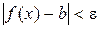 .
.
Записують це так
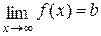 .
.
Приклад 2.7. Довести, що
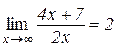 . (2.4)
. (2.4)
Розв’язування. Треба показати, що при довільному ε нерівність
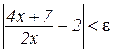 (2.5)
(2.5)
виконуватиметься, як тільки 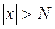 , причому N визначається вибором ε. Нерівність (2.5) еквівалентна нерівності
, причому N визначається вибором ε. Нерівність (2.5) еквівалентна нерівності
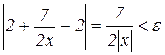 ,
,
яка виконується при
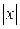 >7/(2ε)=N.
>7/(2ε)=N.
Отже, рівність (2.4) доведено.
Розрізняють також границі
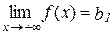 ,
, 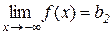 .
.
2.4. Функції, які прямують до нескінченності.
Означення 2.7. Функція 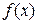 прямує до нескінченності або є нескінченно великою при
прямує до нескінченності або є нескінченно великою при 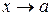 , якщо для кожного як завгодно великого числа M>0 можна знайти число δ>0 таке, що для всіх значень х, які задовольняють умову
, якщо для кожного як завгодно великого числа M>0 можна знайти число δ>0 таке, що для всіх значень х, які задовольняють умову 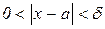 , виконується нерівність
, виконується нерівність 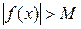 .
.
 Якщо функція
Якщо функція 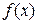 прямує до нескінченності при
прямує до нескінченності при 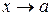 , то записують
, то записують
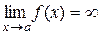 .
.
У випадку, коли при 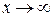 функція
функція 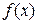 прямує до нескінченності і набуває при цьому тільки додатних або – від’ємних значень, записують відповідно
прямує до нескінченності і набуває при цьому тільки додатних або – від’ємних значень, записують відповідно
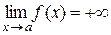
або
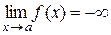 .
.
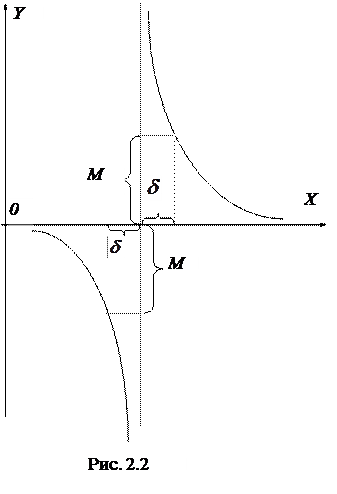
Приклад 8. Покажемо, що
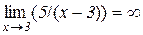 .
.
Дійсно, для довільного M>0 маємо 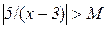 , якщо тільки
, якщо тільки 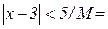 δ. Причому: 5/(x–3)>0, коли x>3, і 5/(x–3)<0, коли x<3, тобто
δ. Причому: 5/(x–3)>0, коли x>3, і 5/(x–3)<0, коли x<3, тобто

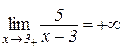 і
і 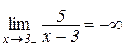
(рис. 2.2).
Якщо функція 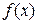 прямує до нескінченності при
прямує до нескінченності при 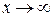 , то записують
, то записують
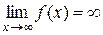 .
.
Наприклад:
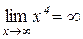 або
або 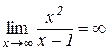 .
.
Зауваження 2.4. Функція 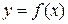 , при
, при 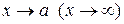 може не мати скінченої або нескінченної границі. Наприклад: y=cosx при
може не мати скінченої або нескінченної границі. Наприклад: y=cosx при 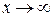 або y=tg(1/x) при
або y=tg(1/x) при 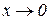 .
.
Обмежені функції.
Означення 2.8. Функція 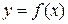 називається обмеженою в заданій області зміни аргументу х, якщо існує додатне число М таке, що для всіх значень х з цієї області виконуватиметься нерівність
називається обмеженою в заданій області зміни аргументу х, якщо існує додатне число М таке, що для всіх значень х з цієї області виконуватиметься нерівність
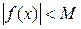 .
.
У випадку, коли не існує вказаного числа М, функція 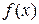 називається необмеженою.
називається необмеженою.
Приклад 2.9. Функція y=cosx, яка визначена на всій числовій осі, тобто при 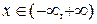 , є обмеженою, тому що для всіх значень аргументу х маємо
, є обмеженою, тому що для всіх значень аргументу х маємо 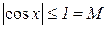 .
.
Означення 2.9. Функція 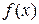 називається обмеженою при
називається обмеженою при 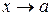 , якщо існує окіл точки а, в якому ця функція обмежена.
, якщо існує окіл точки а, в якому ця функція обмежена.
Означення 2.10. Функція 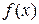 називається обмеженою при
називається обмеженою при 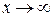 , якщо існує число N таке, що для всіх значень х, які задовольняють умові
, якщо існує число N таке, що для всіх значень х, які задовольняють умові 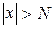 , вона обмежена.
, вона обмежена.
Теорема 2.1. Якщо 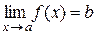 і b є скінчене число, то функція
і b є скінчене число, то функція 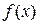 обмежена при
обмежена при 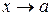 .
.
Доведення. З рівності 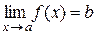 і означення границі функції випливає, що для довільного ε>0 знайдеться число δ>0 таке, що в околі
і означення границі функції випливає, що для довільного ε>0 знайдеться число δ>0 таке, що в околі 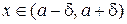 виконуватиметься нерівність
виконуватиметься нерівність
b-ε< 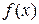 <b+ε або
<b+ε або 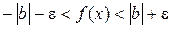 .
.
З останньої нерівності маємо 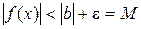 . А це означає, що функція
. А це означає, що функція 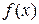 обмежена при
обмежена при 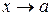
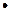
Зауваження 2.5. Нескінченно велика функція є необмеженою.
Теорема 2.2. Якщо
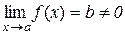 ,
,
то функція y=1/ 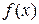 є обмеженою при
є обмеженою при 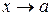 .
.
Доведення. З умови теореми випливає, що при довільному ε>0 існує окіл (а–δ, а+δ) точки а, в якому виконується нерівність 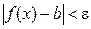 .
.
Зробимо нескладні перетворення останньої нерівності:
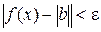 ,
, 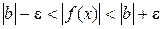 ,
,
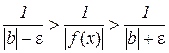 .
.
Якщо взяти, наприклад, 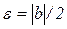 , то отримаємо
, то отримаємо
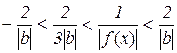
або
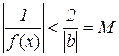 .
.
А це означає, що функція 1/ 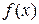 обмежена
обмежена 
Запитаннядля самоконтролю.
1. Дайте означення границі послідовності.
2. Скільки границь може мати змінна величина?
3. Чи кожна змінна величина має границю?
4. Яка змінна величина називається нескінченно великою?
5. Дайте означення границі функції при 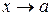 .
.
6. Що таке ліво- і правостороння границі?
7. Чи може існувати границя функції 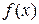 при
при 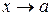 , якщо
, якщо 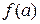 не існує?
не існує?
8. Дайте означення границі функції при 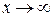 .
.
9. Які функції називаються нескінченно великими?
10. Дайте означення обмеженої функції при 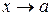 і
і 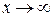 .
.
11. Сформулюйте і доведіть теореми про обмежені функції.
Приклади до розділу 2.
1. Знайти границю змінної величини при 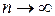 :
:
а) 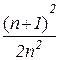 . Відп.: 0,5; б)
. Відп.: 0,5; б) 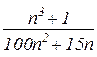 . Відп.:
. Відп.: 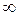 ;
;
в) 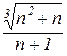 . Відп.: 0; г)
. Відп.: 0; г) 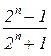 . Відп.: 1;
. Відп.: 1;
д) 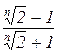 . Відп.: 0.
. Відп.: 0.
2. Знайти границю функції:
а) 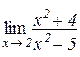 . Відп.:
. Відп.: 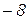 ; б)
; б) 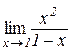 . Відп.:
. Відп.: 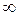 ;
;
в) 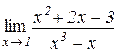 . Відп.: 2; г)
. Відп.: 2; г) 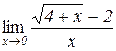 . Відп.: 0,25;
. Відп.: 0,25;
д) 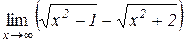 . Відп.: 0; е)
. Відп.: 0; е) 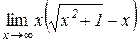 .
.
Відп.: 0,5 або 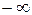 .
.
3. Неперервний ріст популяції 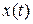 задається функцією від t:
задається функцією від t:
а) 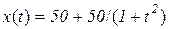 ; в)
; в) 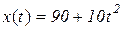 ;
;
б) 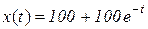 ; г)
; г) 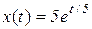 .
.
У кожному випадку знайти початкову популяцію 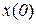 та її граничні розміри.
та її граничні розміри.
4. Популяція бактерій збільшується від початкового розміру до розміру 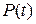 у момент часу t за законом
у момент часу t за законом
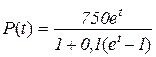 .
.
Знайти 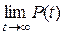 тобто врівноважену популяцію.
тобто врівноважену популяцію.
| <== предыдущая лекция | | | следующая лекция ==> |
| в декартовій прямокутній системі координат. | | | основні властивості. |
Дата добавления: 2016-05-05; просмотров: 1489;
