в декартовій прямокутній системі координат.
Схема повного дослідження функції.
На підставі матеріалу, викладеного в розділах 11 і 12, можна запропонувати наступну схему дослідження функції.
Знаходимо:
1) область існування функції;
2) функція є парною чи непарною;
3) точки розриву функції;
4) інтервали монотонності функції;
5) екстремуми функції;
6) інтервали опуклості та вгнутості графіка, точки пергину;
7) асимптоти графіка функції: а) вертикальні; б) похилі.
 |
13.2. Дослідження і побудова графіка функції, заданої
в декартовій прямокутній системі координат.
Приклад 13.1. Провести повне дослідження функції
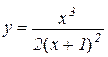
та побудувати її графік.
Розв’язання. 1) Область визначення функції:
 .
.
2) Парність і непарність функції. Так як
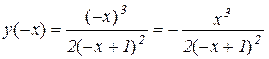 ,
,
то, 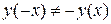 і
і 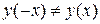 , тобто функція є ні парною, ні непарною.
, тобто функція є ні парною, ні непарною.
3) Точки розриву функції. З області існування функції робимо висновок, що функція неперервна в усіх точках, крім точки 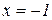 . В точці
. В точці 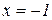 функція має розрив 2-го роду, тому що
функція має розрив 2-го роду, тому що
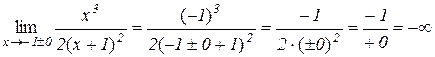 .
.
4) Інтервали монотонності функції:
а) знаходимо похідну
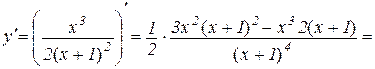
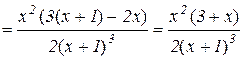 ;
;
б) критичні точки функції:
точки, де 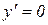 :
:
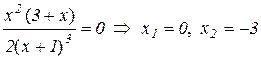 ;
;
точки, де друга похідна не існує:
 ;
;
в) інтервали монотонності функції:
5) Функція зростає на інтервалах 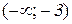 і
і 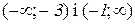 , а спадає –
, а спадає – 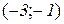 .
.
Екстремуми функції. З рис. 13.1 видно, що функція має один екстремум: в точці 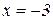 функція набуває максимуму
функція набуває максимуму
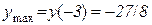 .
.
В точці 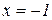 функція не існує.
функція не існує.
6) Інтервали опуклості і вгнутості, точки перегину:
а) знаходимо другу похідну

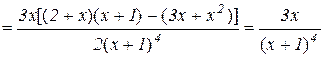 .
.
б) критичні точки першої похідної:
точки, де 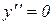 :
:
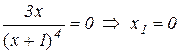 ;
;
  |
точки, де
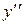 не існує:
не існує:
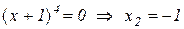 .
.
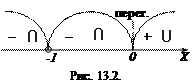 в) інтервали опуклості і вгнутості та точки перегину (рис. 13.2):
в) інтервали опуклості і вгнутості та точки перегину (рис. 13.2):
Функція опукла на інтервалах 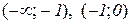 і вгнута –
і вгнута – 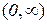 . Точка з координатами
. Точка з координатами 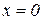 і
і 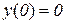 є точкою перегину.
є точкою перегину.
7) Асимптоти:
а) вертикальні асимптоти: з п.3) видно, що пряма 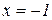 є вертикальною асимптотою;
є вертикальною асимптотою;
б) похилі асимптоти: вони мають вигляд 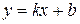 . Знайдемо
. Знайдемо 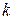 і
і 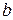 :
:

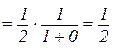 ;
;
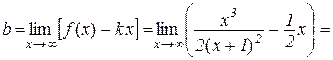
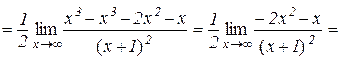
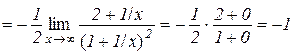 .
.
Таким чином, пряма 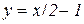 є похилою асимптотою.
є похилою асимптотою.
8) Будуємо графік. Для побудови графіка складаємо допоміжну таблицю
| х | -¥ | (-¥,-3) | -3 | (-3;-1) | -1-0 | -1+0 | (-1;0) | 0 | (0;+¥) | +¥ |
| f(x) | 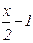
| 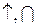
| 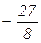
| 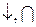
| –¥ | –¥ | 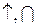
| 0 | 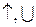
| 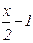
|
де в першому рядку показані всі інтервали, на які критичні точки функції і першої похідної ділять числову вісь, а також граничні значення 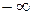 ,
, 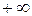 і
і 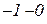 ,
, 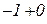 . В другому рядку показуємо поведінку функції на цих інтервалах, граничні значення функції при
. В другому рядку показуємо поведінку функції на цих інтервалах, граничні значення функції при 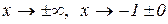 та
та 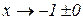 , значення в критичних точках.
, значення в критичних точках.
Спочатку відкладаємо асимптоти (рис. 13.3), а потім – участки графіка окремо на кожному інтервалі 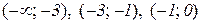 ,
, 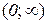 . Покажемо це на прикладі інтервалу
. Покажемо це на прикладі інтервалу  . З таблиці визначаємо, як поводить себе функція на кінцях інтервалу: ліворуч, тобто, при
. З таблиці визначаємо, як поводить себе функція на кінцях інтервалу: ліворуч, тобто, при 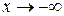 крива нескінченно наближається до похилої асимптоти – положення А, а праворуч –
крива нескінченно наближається до похилої асимптоти – положення А, а праворуч – 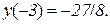 – положення В. Точки А і В з’єднуємо зростаючою опуклою кривою.
– положення В. Точки А і В з’єднуємо зростаючою опуклою кривою.
Аналогічно проводиться побудова на інших інтервалах.
13.3. Дослідження і побудова графіка функції заданої
Параметрично.
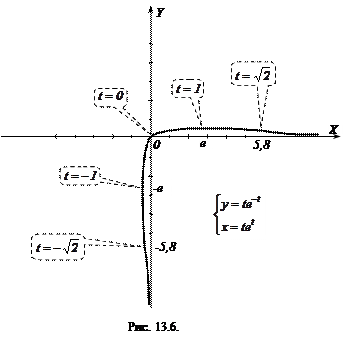
Приклад 13.2. Дослідити функцію
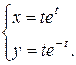
і побудувати її графік
Розв’язання. 1) Область визначення. Функції х і у існують за всіх значень 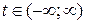
2) Знайдемо поведінку функцій х і у при 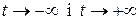 :
:
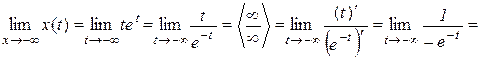
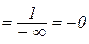 ,
,
 ,
,
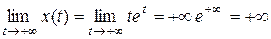 ,
,
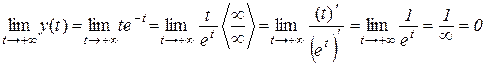 .
.
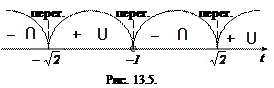 |
При обчисленні першої і останньої границі, ми використали правило Лопіталя.
3) Функції 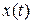 і
і 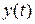 неперервні за всіх значень
неперервні за всіх значень 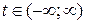 .
.
4) Інтервали монотонності:
а) знаходимо першу похідну
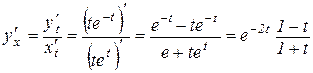 ;
;
б) критичні точки функції 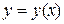 похідної:
похідної:
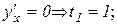 ;
;
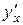 не існує при
не існує при  ;
;
в) інтервали монотонності (рис. 13.4)
Таким чином, функція 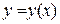 , яка задана параметрично, зростає на інтервалі
, яка задана параметрично, зростає на інтервалі 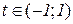 і спадає на інтервалах
і спадає на інтервалах 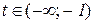 та
та 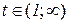 ;
;
г) знайдемо координати точок, які відповідають критичним значенням параметра t:
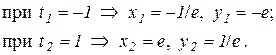
5) Інтервали опуклості і вгнутості:
а) знаходимо другу похідну:
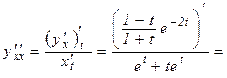
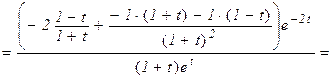
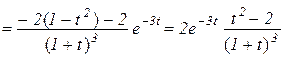 .
.
б) критичні точки першої похідної:
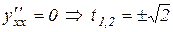 ;
;
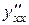 на існує при
на існує при 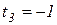 .
.
в) інтервали опуклості і вгнутості (рис. 13.5):
Таким чином, функція 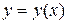 опукла на інтервалах
опукла на інтервалах 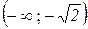 та
та 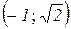 і вгнута –
і вгнута – 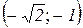 та
та 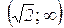 ;
;
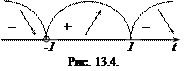 г) знаходимо координати точок, які відповідають критичним значенням параметра t для першої похідної:
г) знаходимо координати точок, які відповідають критичним значенням параметра t для першої похідної:
при 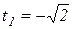 маємо
маємо
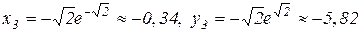 ;
;
при 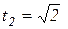 маємо
маємо
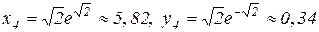 .
.
Для побудови графіка складаємо допоміжну таблицю.
Тепер будуємо графік на кожному з інтервалів 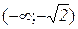 ,
, 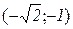 ,
, 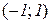 ,
, 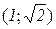 ,
, 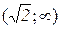 окремо.
окремо.
| T | -¥ | (-¥,- 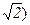
| - 
| (- 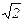 ;-1) ;-1)
| -1 | (-1;1) | 1 | (1; 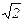 ) )
| 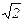
| ( 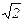 ,¥) ,¥)
| ¥ |
| х(t) | 0 | -0,3 | -e-1 | e | 5,8 | ¥ | |||||
| y(t) | -¥ | -5,8 | -e | e-1 | 0,3 | 0 | |||||
| y(x) | 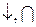
| 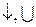
| 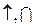
| 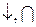
| 
|
Наприклад, на інтервалі 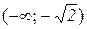 крива спадає, опукла і з’єднує (якщо йти в напрямку зростання змінної х) точку з координатами
крива спадає, опукла і з’єднує (якщо йти в напрямку зростання змінної х) точку з координатами 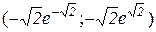 і граничне положення
і граничне положення 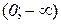 . Аналогічно – для інших інтервалів (рис. 13.6).
. Аналогічно – для інших інтервалів (рис. 13.6).
Запитання для самоконтролю.
1. Наведіть схему повного дослідження функції.
2. Яка різниця між схемами дослідження функцій заданих в явному вигляді і – параметрично?
Прикладидо розділу 13.
Провести повне дослідження функції і побудувати її графік:
 |
а)
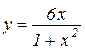 ; б)
; б)  ; в)
; в) 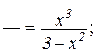 ;
;
г) 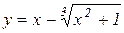 ; д)
; д) 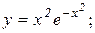 ; е)
; е) 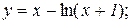 ;
;
є) 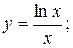 ; ж)
; ж) 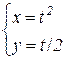 ; з)
; з) 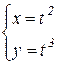 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Поняття опуклості і вгнутості графіка функції. | | | Границя числової послідовності. |
Дата добавления: 2016-05-05; просмотров: 1043;
