Неперервність функції в точці.
Розглянемо визначену в деякому околі точки х=х0 функцію y=f(x). Нехай y0=f(x0). Надамо значенню аргументу х0 деякий додатний (або від’ємний) приріст 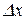 . Новому значенню аргументу
. Новому значенню аргументу 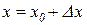 відповідатиме нове значення функції
відповідатиме нове значення функції  , де
, де  – приріст функції. Очевидно, що
– приріст функції. Очевидно, що
 .
.
Означення 5.1. Функція y=f(x) називається неперервною в точці х=х0, якщо вона визначена в деякому околі точки х0 і якщо
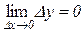
або
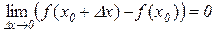 . (5.1)
. (5.1)
Приклад 5.1. Покажемо, що функція  неперервна в довільній точці х0.
неперервна в довільній точці х0.
Дійсно,
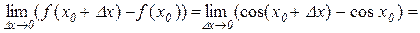
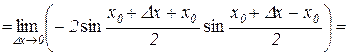

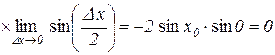 .
.
Аналогічно можна показати неперервність кожної елементарної функції в точках де вона існує. Сформулюємо без доведення таку теорему.
Теорема 5.1. Кожна елементарна функція неперервна в усіх точках, де вона визначена 
З умови неперервності (5.1) слідує, що
 або
або  .
.
Але  , тому
, тому
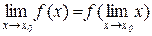 (5.2)
(5.2)
Таким чином, щоб знайти границю неперервної функції при 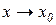 , досить підставити в функцію замість аргументу х його граничне значення х0.
, досить підставити в функцію замість аргументу х його граничне значення х0.
Приклад 5.2. Покажемо, що
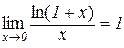 .
.
Дійсно,
 .
.
Оскільки  і функція
і функція 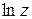 неперервна при z>0, а, значить, і при z=e, то з (5.2) випливає, що
неперервна при z>0, а, значить, і при z=e, то з (5.2) випливає, що
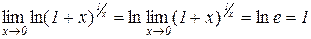 .
.
5.2. Неперервність функції на проміжку.
Означення 5.2. Якщо функція неперервна в кожній точці інтервалу (a, b), то кажуть, що вона неперервна на цьому інтервалі.
Означення 5.3. Якщо функція y=f(x) визначена в точці х=а і при цьому  , то кажуть, що в точці х=а функція f(x) неперервна праворуч.
, то кажуть, що в точці х=а функція f(x) неперервна праворуч.
Означення 5.4. Якщо функція y=f(x) визначена в точці х=b і при цьому 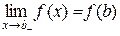 , то кажуть ,що в точці х=b функція f(x) неперервна ліворуч.
, то кажуть ,що в точці х=b функція f(x) неперервна ліворуч.
Означення 5.5. Якщо функція f(x) неперервна на інтервалі (а,b) і неперервна на кінцях інтервалу (а, b) відповідно праворуч і ліворуч, то кажуть, що дана функція неперервна на відрізку [a, b].
З означення неперервності функції в точці випливає, що функція y=f(x) неперервна в точці х=х0 , якщо вона визначена в цій точці і виконується рівність
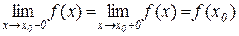 . (5.3)
. (5.3)
Означення 5.6. Якщо в якійсь точці для функції не виконується хоча б одна з умов неперервності, то функція називається розривною в цій точці, а сама точка називається точкою розриву.
Означення 5.7. Якщо існують скінчені границі
 ,
, 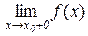 ,
,
але функція f(x) в точці х=х0 не визначена або рівність (5.3) не виконується, то точку х=х0 називають точкою розриву 1-го роду.
Цей розрив ще називають усувним, в точці розриву відбувається скінчений стрибок.
Усі інші точки розриву називають точками розриву 2-го роду.
5.3. Приклади дослідження на неперервність.
Приклад 5.3. Дослідити на неперервність функцію 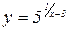 та побудувати її схематичний графік.
та побудувати її схематичний графік.
 Розв’язування. Задана функція визначена на всій числовій осі крім точки х=3. Вона є композицією двох основних елементарних функцій (степеневої і показникової), тому є елементарною функцією (див. означення 1.16) і за теоремою 5.1 – неперервною при
Розв’язування. Задана функція визначена на всій числовій осі крім точки х=3. Вона є композицією двох основних елементарних функцій (степеневої і показникової), тому є елементарною функцією (див. означення 1.16) і за теоремою 5.1 – неперервною при 
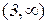 . В точці х=3 функцій має розрив. Для визначення роду точки розриву та побудови графіка знайдемо ліво- й правосторонню границі функції в точці х=3:
. В точці х=3 функцій має розрив. Для визначення роду точки розриву та побудови графіка знайдемо ліво- й правосторонню границі функції в точці х=3:
 ;
;
 .
.
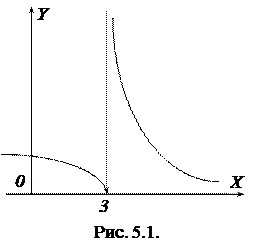
Таким чином, в точці х=3 функція має розрив 2-го роду (рис. 5.1).
Приклад 4. Дослідити на неперервність функцію
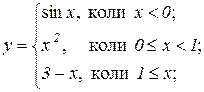 (5.4)
(5.4)
 та побудувати її графік.
та побудувати її графік.
Розв’язування. Функції  , х2, х–3, за допомогою яких задається функція у, є неперервними на всій числовій осі. Тому функція у неперервна в усіх точках, крім, можливо, точок х=0 і х=1. В цих точках проведемо дослідження на неперервність за допомогою рівності (5.3):
, х2, х–3, за допомогою яких задається функція у, є неперервними на всій числовій осі. Тому функція у неперервна в усіх точках, крім, можливо, точок х=0 і х=1. В цих точках проведемо дослідження на неперервність за допомогою рівності (5.3):
а) точка х0=0:
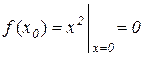 ,
,
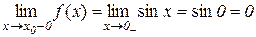 ,
,
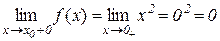 .
.
Таким чином,  і функція неперервна в точці х=0;
і функція неперервна в точці х=0;
б) точка х0=1:
 ,
,
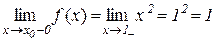 ,
,
 .
.
Таким чином, 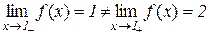 і, значить, функція в точці х=1 має розрив 1-го роду.
і, значить, функція в точці х=1 має розрив 1-го роду.
Схематичний графік функції (5.4) показано на рис. 5.2.
5.4. Властивості неперервних функцій.
 Наведемо у вигляді теорем (без доведення) деякі основні властивості неперервних на відрізку функцій.
Наведемо у вигляді теорем (без доведення) деякі основні властивості неперервних на відрізку функцій.
Теорема 5.2. Неперервна на відрізку [a, b] функція досягає на цьому відрізку хоча б один раз своє найменше m і найбільше М значення 
Зміст цієї теореми проілюстровано на рис. 5.3.
 Зауваження. 5.1 Твердження теореми хибне, якщо розглядати монотонну функцію неперервну на інтервалі (а, b). В цьому випадку функція не має найменшого і найбільшого значень.
Зауваження. 5.1 Твердження теореми хибне, якщо розглядати монотонну функцію неперервну на інтервалі (а, b). В цьому випадку функція не має найменшого і найбільшого значень.
Для розривних функцій твердження теореми може бути як хибним так і справедливим.
Теорема 5.3.Якщо неперервна на відрізку [a, b] функція f(x) на кінцях цього відрізка набуває різних по знаку значень, то на інтервалі (a, b) існує хоча б одна точка х=с, в якій функція приймає значення 0, тобто f(c)=0, де 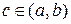
Ця теорема має простий геометричний зміст (рис. 5.4). Неможливо з’єднати точки М1(a, f(a)) і М2(b, f(b)) неперервною лінією не перетнувши жодного разу вісь ОХ.
Приклад 5.5. Функція
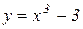
неперервна на відрізку [-2; 3] і

 ,
,
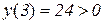 .
.
Отже, на цьому відрізку існує точка, де дана функція дорівнює нулю. Дійсно,  при
при  .
.
Теорема 5.4. Якщо неперервна на відрізку [a, b] функція f(x) приймає на кінцях цього відрізка різні значення, тобто
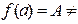
 ,
,
 то для будь-якого числа μ, розміщеного між значеннями А і В, існує хоча б одна точка
то для будь-якого числа μ, розміщеного між значеннями А і В, існує хоча б одна точка 
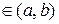 така, що
така, що 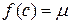
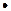
Зміст цієї теореми ілюструє рис. 5.5. Довільна пряма 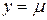 перетинає графік функції хоча б один раз.
перетинає графік функції хоча б один раз.
Наслідок 5.4. Якщо функція 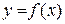 неперервна на відрізку [a, b], то на ньому вона набуває хоча б один раз будь-яке значення, розміщене між найменшим і найбільшим значеннями.
неперервна на відрізку [a, b], то на ньому вона набуває хоча б один раз будь-яке значення, розміщене між найменшим і найбільшим значеннями.
Дійсно, нехай 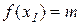 і
і 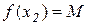 , тоді за відрізок
, тоді за відрізок  можна взяти відрізок
можна взяти відрізок 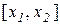 або
або 
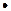
Зауваження. 5.2. Теорема 5.3 є частинним випадком теореми 5.4 при 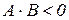 і
і  .
.
Запитання для самоконтролю.
1. Дайте означення функції неперервної в точці.
2. Теорема про неперервність елементарних функцій.
3. Дайте означення функції неперервної на інтервалі, на відрізку.
4. Запишіть умову неперервності функції в точці.
5. Типи точок розриву функції.
6. Основні властивості функцій, неперервних на відрізку.
Приклади до розділу 5.
1. Знайти точки розриву функції:
 . Відп.:
. Відп.:  .
.
2. Дослідити функцію 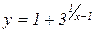 на неперервність і побудувати її схематичний графік.
на неперервність і побудувати її схематичний графік.
3. Знайти при яких значеннях А і В функція 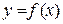 буде неперервною і побудувати її графік, якщо
буде неперервною і побудувати її графік, якщо
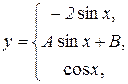

| <== предыдущая лекция | | | следующая лекция ==> |
| аргументу. Число е. | | | Порівняння нескінченно малих. |
Дата добавления: 2016-05-05; просмотров: 4178;
