Порівняння нескінченно малих.
Нехай функції 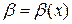 і
і 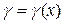 – нескінченно малі при
– нескінченно малі при 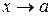 або
або 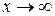 .
.
Означення 6.1. Якщо відношення 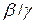 має скінчену границю відмінну від нуля, тобто
має скінчену границю відмінну від нуля, тобто
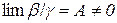 і
і 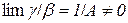 ,
,
то 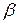 і
і 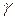 називають нескінченно малими одного порядку.
називають нескінченно малими одного порядку.
Приклад 6.1. Функції 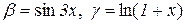 при
при 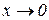 є нескінченно малими одного порядку, тому що
є нескінченно малими одного порядку, тому що
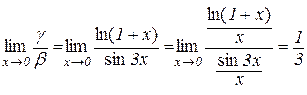
(див. приклад 5.2).
Приклад 6.2. При 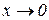 нескінченно малі
нескінченно малі
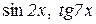 ,
, 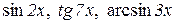 ,
, 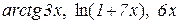
є нескінченно малими одного порядку.
Доведення проводиться аналогічно попередньому прикладу з використанням наслідків до першої “чудової” границі (див. розділ 4.1).
Означення 6.2. Якщо відношення двох нескінченно малих 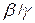 прямує до нуля, тобто
прямує до нуля, тобто 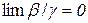 , то нескінченно мала
, то нескінченно мала 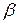 називається нескінченно малою величиною вищого, ніж нескінченно мала
називається нескінченно малою величиною вищого, ніж нескінченно мала 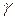 , порядку малості, а нескінченно мала
, порядку малості, а нескінченно мала 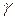 називається нескінченно малою нищого, ніж нескінченно мала
називається нескінченно малою нищого, ніж нескінченно мала 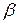 , порядкумалості.
, порядкумалості.
Приклад 6.3. Нехай 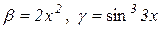 . При
. При 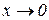 нескінченно мала
нескінченно мала 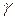 є нескінченно малою вищого, ніж нескінченно мала
є нескінченно малою вищого, ніж нескінченно мала 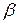 , порядку малості, оскільки
, порядку малості, оскільки
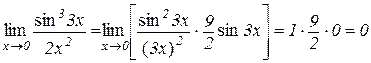 .
.
Означення 6.3. Нескінченно мала 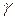 називається нескінченно малою k-го порядку відносно нескінченно малої
називається нескінченно малою k-го порядку відносно нескінченно малої 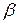 , якщо
, якщо 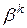 і
і 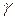 нескінченно малі одного порядку, тобто якщо
нескінченно малі одного порядку, тобто якщо
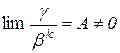 і
і  .
.
Приклад 6.4. Якщо 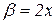 і
і 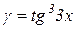 , то при
, то при 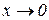 нескінченно мала
нескінченно мала 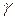 є нескінченно малою третього порядку малості відносно нескінченно малої
є нескінченно малою третього порядку малості відносно нескінченно малої 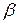 , тому що
, тому що
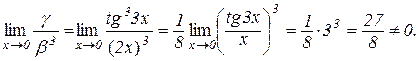
6.2.Еквівалентні нескінченно малі.
Означення 6.4. Якщо відношення двох нескінченно малих 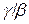 прямує до 1, тобто
прямує до 1, тобто 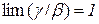 , то нескінченно малі
, то нескінченно малі 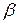 і
і 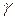 називають еквівалентними нескінченно малими і позначають
називають еквівалентними нескінченно малими і позначають 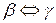 .
.
Приклад 6.5. Нескінченно малі 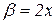 і
і 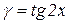 при
при 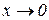 є еквівалентними нескінченно малими, через те що
є еквівалентними нескінченно малими, через те що
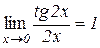 .
.
Приклад 6.6. Нескінченно малі 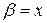 і
і 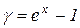 при
при 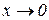 є еквівалентними нескінченно малими, оскільки
є еквівалентними нескінченно малими, оскільки
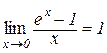 .
.
Дійсно, зробимо заміну 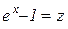 , тоді
, тоді 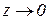 при
при 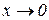 і
і 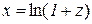 . Отримаємо:
. Отримаємо:
 .
.
Теорема 6.1. Для еквівалентності двох нескінченно малих 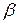 і
і 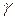 необхідно і достатньо, щоб їх різниця, тобто
необхідно і достатньо, щоб їх різниця, тобто 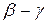 , була нескінченно малою вищого, ніж
, була нескінченно малою вищого, ніж 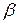 і ніж
і ніж 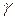 , порядку малості.
, порядку малості.
Доведення. Необхідність. Нехай 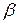 і
і 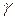 еквівалентні нескінченно малі. Покажемо, що їх різниця
еквівалентні нескінченно малі. Покажемо, що їх різниця 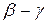 є нескінченно малою вищого, ніж
є нескінченно малою вищого, ніж 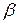 і ніж
і ніж 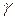 , порядку малості. Дійсно,
, порядку малості. Дійсно,
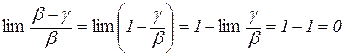 .
.
Аналогічно для нескінченно малої 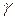 .
.
Достатність. Нехай різниця нескінченно малих 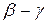 є нескінченно малою вищого, ніж
є нескінченно малою вищого, ніж 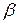 і ніж
і ніж 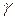 , порядку малості. Покажемо, що
, порядку малості. Покажемо, що 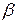 і
і 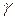 еквівалентні нескінченно малі. Дійсно,
еквівалентні нескінченно малі. Дійсно,
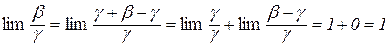 .
.
Таким чином, теорему доведено 
Приклад 6.7. Нехай 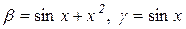 і
і 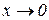 . Нескінченно малі
. Нескінченно малі 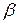 і
і 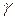 еквівалентні, оскільки
еквівалентні, оскільки
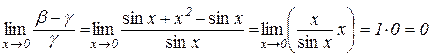 ,
,
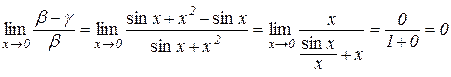 .
.
Наведемо список деяких еквівалентних нескінченно малих при 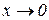 :
: 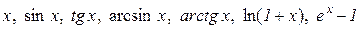 .
.
Запитання для самоконтролю.
1. Дайте означення нескінченно малих одного порядку малості.
2. В якому випадку нескінчено мала 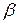 називається нескінченно малою вищого порядку по відношенню до нескінченно малої
називається нескінченно малою вищого порядку по відношенню до нескінченно малої 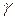 ?
?
3. Дайте означення нескінченно малої k-го порядку малості.
4. Які нескінченно малі називаються еквівалентними.
5. Сформулюйте необхідну і достатню умову еквівалентності двох нескінченно малих.
Приклади до розділу 6.
1. Знайти при 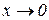 порядок малості відносно х таких величин:
порядок малості відносно х таких величин:
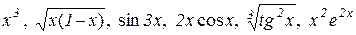 .
.
2. З нескінченно малих при 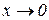 величин вибрати еквівалентні х:
величин вибрати еквівалентні х:
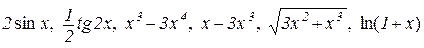 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Неперервність функції в точці. | | | Означення похідної. |
Дата добавления: 2016-05-05; просмотров: 3439;
