Означення похідної.

Нехай функція 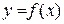визначена в деякому інтервалі 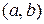. Надамо значенню аргументу 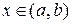приріст 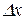такий, що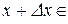 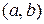, тоді функція у дістане деякий приріст

.

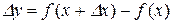Означення 7.1. Границя відношення приросту функції 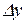до приросту аргументу 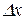при прямуванні останнього до нуля, якщо вона існує, називається похідною функції 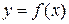і позначається 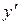, 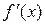або .

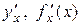Отже, з означення похідної випливає, що

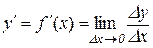або .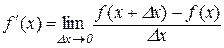

Процес знаходження похідної функції називається диференціюванням функції.

Приклад 7.1. Знайти похідну функції 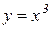та її значення в точці х=4.

Розв’язування. За означенням похідної

,

.

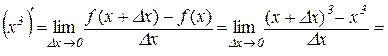
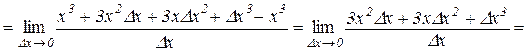
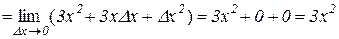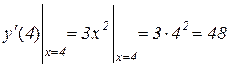7.2. Геометричний зміст похідної.

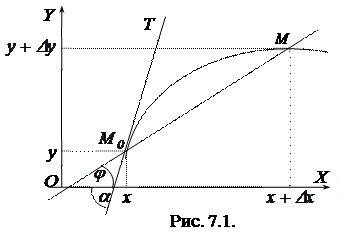Нехай функція 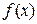задає в декартовій прямокутній системі координат криву 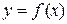(рис. 7.1). Значенню аргументу х на кривій відповідає точка 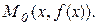Надамо аргументу приріст 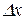, тоді значенню аргументу 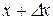відповідатиме точка 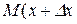, 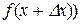кривої. Проведемо січну 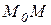і позначимо кут, який утворює дана січна з віссю ОХ , через 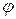. Складемо відношення 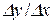. Згідно рис. 7.1

.

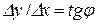Тепер спрямуємо 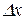до нуля, тоді точка М прямуватиме вздовж кривої 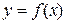до точки М₀ .

Означення 7.2. Якщо при наближенні точки М вздовж кривої 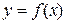до точки М₀ січна М₀М наближається до певного граничного положення М₀Т, то пряму М₀Т називають дотичною до кривої 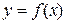в точці М₀ .

Позначимо кут, який утворює дотична М₀Т з віссю ОХ, через 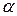, тоді відповідно до означення похідної матимемо

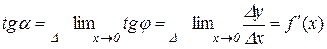
або

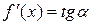. (7.1)

Таким чином, значення похідної 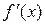при значенні аргументу х дорівнює тангенсу кута нахилу до осі ОХ дотичної у відповідній точці .

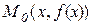7.3. Механічний зміст похідної.

Нехай задано закон прямолінійного руху матеріальної точки:

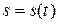. (7.2)

Переміщення s відраховується від деякого початкового положення М₀ (рис. 7.2). Тоді в деякий момент часу t точка перебуватиме в положенні М на відстані 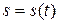від точки М₀ , а в момент часу 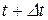– в точці М₁ на відстані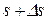 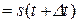від точки М₀ . Середня швидкість точки за час 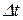дорівнює

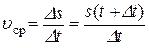. (7.3)

Вона характеризує швидкість точки на відрізку ММ₁ з певною точністю, яка залежить від величини інтервалу 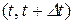: чим менший інтервал часу, тим ближче швидкість 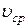до швидкості 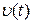в точках на заданому відрізку. Щоб обчислити точне значення швидкості в момент часу t, перейдемо до границі в (7.3) при :

.

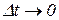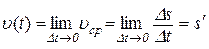Таким чином, швидкість точки в даний момент часу дорівнює похідній по часу від функції, яка задає закон руху цієї точки:

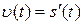. (7.4)

Приклад 7.2. Нехай популяція в момент часу t (в днях) нараховує p(t) осіб: 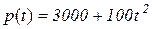. Знайти швидкість зростання популяції: а) в довільний момент часу t; б) в момент часу t=1 день.

Розв’язування. Маємо

а)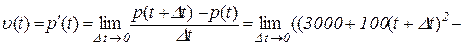

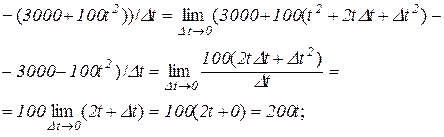
б) .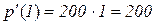

7.4.Диференційовані функції.

Означення 7.3. Функція 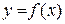називається диференційованою в точці 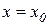, якщо в цій точці вона має скінчену похідну, тобто якщо

.

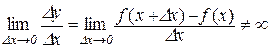Означення 7.4. Функція називається диференційованою на інтервалі 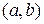, якщо вона диференційована в кожній точці цього інтервалу.

Теорема 7.1. Якщо функція 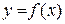диференційована в точці х=х₀ , то в цій точці вона неперервна.

Доведення. Справді, якщо

,

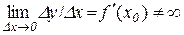то за теоремою 3.1 маємо

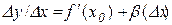або ,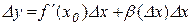

де 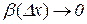при 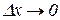. З останньої рівності отримаємо

,

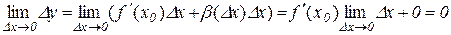а це означає, що функція f(x) неперервна в точці х₀ (див. означення 5.1)

З теореми 7.1 випливає, що в точках розриву функція не може мати похідну. Зворотне твердження хибне: недиференційована в точці функція може бути неперервною в даній точці.

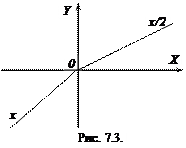
Приклад 7.3. Розглянемо функцію

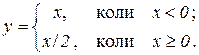
Вона неперервна в точці х₀=0 (рис. 7.3). Але похідна в цій точці не існує. Це дуже легко показати за допомогою дотичної. Кутовий коефіцієнт дотичної в будь-якій точці, розміщеній лівіше точки х=0, дорівнює 1, а – правіше точки х=0, дорівнює 1/2. Тобто під час переходу через точку х=0 відбувається стрибок похідної 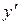і в точці х=0 границя 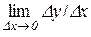не існує.

7.5.Основні властивості похідної.

Теорема 7.2. Похідна сталої рівна нулю, тобто, якщо у=С= =const, то .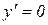

Доведення. Функція у=С приймає одне й теж значення при довільних значеннях аргументу х. Тому для будь-якої точки х₀ маємо у(х₀)=С і 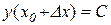, а значить,

.

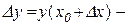
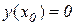Таким чином,

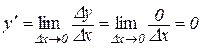
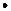
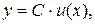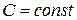Теорема 7.3. Сталий множник можна виносити за знак похідної, тобто, якщо де , то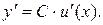

Доведення. Аналогічно попередній теоремі маємо

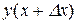
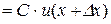
і

,

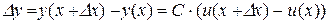тому

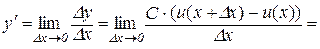
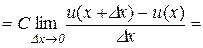
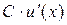
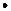
Теорема 7.4. Похідна суми скінченого числа диференційованих функцій дорівнює сумі похідних цих функцій, тобто (для трьох доданків), якщо 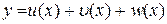, то

.

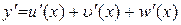Доведення. Маємо

,

,

,

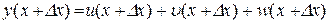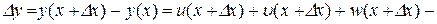
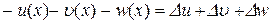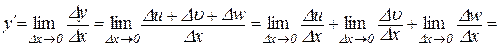
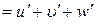тобто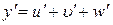

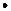
Теорема 7.5. Похідна добутку двох диференційованих функцій дорівнює сумі добутків похідної першого множника на другий і першого множника на похідну другого, тобто, якщо

,

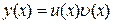то

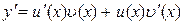або .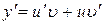

Доведення. Аналогічно попередній теоремі маємо

,

,

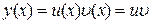
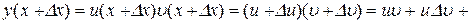
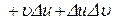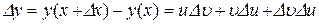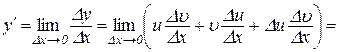
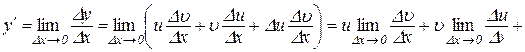
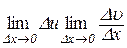. (7.5)

Множники u і 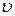не залежать від 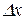, тому їх можна винести за знак границі.

Розглянемо в (7.5) третій доданок:

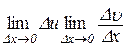. (7.6)

Функція u диференційована, тому за теоремою 7.1 вона неперервна, тобто 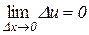. Крім того, з диференційованості функції 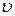випливає, що

,

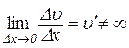а, значить, добуток (7.6) за теоремою 3.4 дорівнює нулю. Отже,

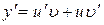
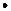
Теорема 7.6. Якщо 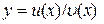і u(x), 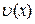– диференційовані функції, то

.

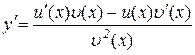Доведення. Маємо

,

,

.

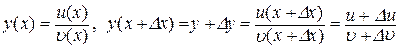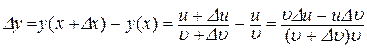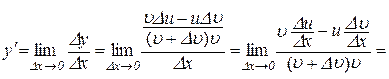
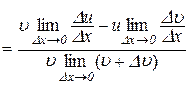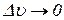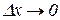Оскільки при , то

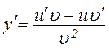
Запитання для самоконтролю.

1. Дайте означення похідної.

2. Який геометричний зміст похідної?

3. Який механічний зміст?

4. Дайте означення дотичної до кривої.

5. Яка функція називається диференційованою в точці, на інтервалі?

6. Сформулюйте теорему про зв’язок між неперервністю і диференційованістю функції в точці.

7. Чи випливає з неперервності функції в точці її диференційованість в цій точці?

8. Сформулюйте основні властивості похідної і доведіть їх.

Приклади до розділу 7.

1. Знайти похідну функцій:

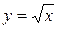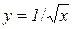а) у=1/х; б) ; в) ; г) .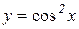

2. Знайти тангенси кута нахилу дотичних до кривих:

а) 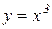, якщо х₁=1, х₂=0, ;

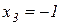б) 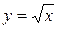, якщо х₁=2;

в) 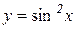, якщо , .

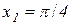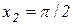3. Задано закон прямолінійного руху s=t³+3/t. Знайти середню швидкість руху за проміжок часу від t=4с до 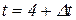с, де 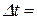0,1; 0,03 і швидкість в момент часу t=1c.

4. Задана функція у=х². Знайти .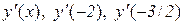

5. Доведіть справедливість співвідношення

,

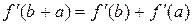де .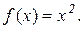

6. Залежність між кількістю речовини х, що отримують в деякій хімічній реакції, і часом t задається рівнянням 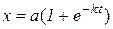, де а – початкова кількість речовини. Знайти швидкість реакції в момент часу t.