Геометричний зміст похідної.
Граничне положення січної 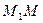 при прямуванні точки
при прямуванні точки 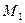 до точки
до точки 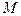
По кривій називають дотичною до кривої в точці М
Нехай крива, задана рівнянням 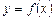 , має дотичну в точці М (х, у).
, має дотичну в точці М (х, у).
Геометричний зміст похідної функції в певній точці : похідна 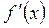 чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х:
чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х: 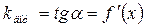
Рівняння дотичної і нормалі до плоскої кривої.
 Нехай функція у = f (t) означена і неперервна на деякому проміжку [a; b]..
Нехай функція у = f (t) означена і неперервна на деякому проміжку [a; b]..

Рівняння дотичної:
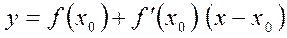
де 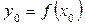 - значення функції в точці
- значення функції в точці 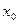
Нормаллю до графіка функції в точці М0 називається перпендикуляр, проведений до дотичної в цій точці.
Рівняння нормалі: 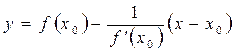
Приклад. Знайти рівняння дотичної та нормалі до графіка функції у = х2 у точці з абсцисою х0 = – 3.
1) знаходимо похідну від заданої функції 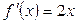 ;
;
2) знаходимо значення похідної в точці х0 = – 3: 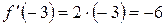 ;
;
3) знаходимо значення функції в точці х0 = – 3: 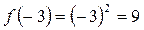 .
.
4) рівняння дотичної запишеться так: 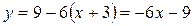
5) рівняння нормалі запишеться так: 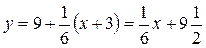
Основні правила диференціювання.
Якщо 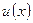 та
та 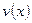 - деякі диференційовані функції, то
- деякі диференційовані функції, то
1) 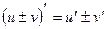
2) 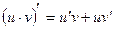
3) 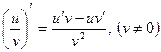
4) 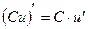
5) 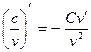
Таблиця похідних
1) 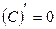
2) 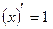
3) 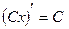
4) 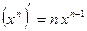
5) 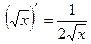
6) 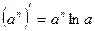
7) 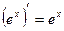
8) 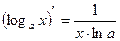
9) 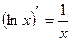
10) 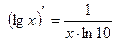
11) 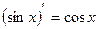
12) 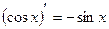
13) 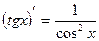
14) 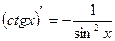
15) 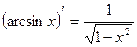
16) 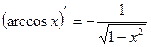
17) 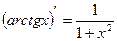
18) 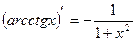
Дата добавления: 2016-06-02; просмотров: 1320;
