Формула Ньютона – лейбніца.
Якщо у функції f(x) існує первісна F(x), то
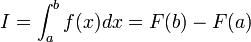
Використання інтегралів для обчислення площі плоских фігур
| № п/п | Назва поняття. | Геометричне зображення | Формула для обчислення. |
| 1. |  Площа криволінійної трапеції, якщо Площа криволінійної трапеції, якщо 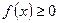 на відрізку на відрізку 
| 
| 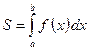
|
| 2. | Площа криволінійної трапеції, якщо  на відрізку на відрізку 
| 
| 
|
| 3. | Якщо фігура обмежена графіками неперервних на відрізку  функціями функціями 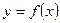 і і 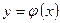 , при чому , при чому 
| 
| 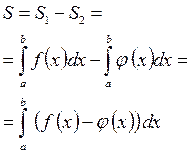
|
| 4. |  Якщо функціями Якщо функціями 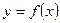 кілька разів змінює знак на відрізку кілька разів змінює знак на відрізку  , то інтеграл для обчислення площі на всьому відрізку , то інтеграл для обчислення площі на всьому відрізку  розбиваємо на частини. Інтеграл буде додатній на тих частинах, де розбиваємо на частини. Інтеграл буде додатній на тих частинах, де 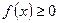 і від’ємний там де і від’ємний там де  . .
| 
| 
|
Приклади для розв’язування.
1. Знайти невизначені інтеграли.
1) 
2) 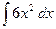
3) 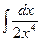
4) 
5) 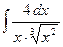
6) 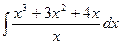
7) 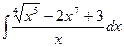
8) 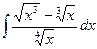
9) 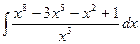
10) 
11) 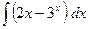
12) 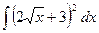

13) 
14) 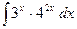
15) 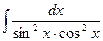
16) 
17) 
18) 
19) 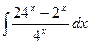
20) 
21) 
22) 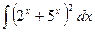
23) 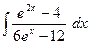
24) 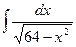
25) 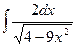
26) 
27) 
28) 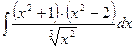
29) 
30) 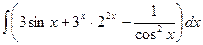
31) 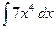
32) 
33) 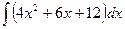
34) 
35) 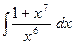
36) 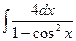
37) 
38) 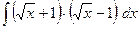
39) 
40) 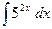
41) 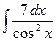
42) 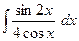
43) 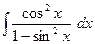
44) 
45) 

2.** Знайти невизначені інтеграли.
1) 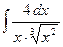
2) 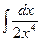
3) 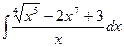
4) 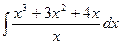
5) 
6) 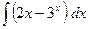
7) 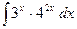
8) 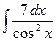
9) 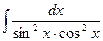
10) 
11) 
12) 
13) 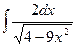
14) 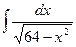
15) 
16) 
17) 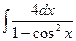
18) 
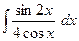
3.* Знайти невизначений інтеграл методом заміни змінної.
1. 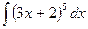
2. 
3. 
4. 
5. 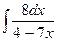
6. 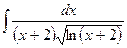
7. 
8. 
9. 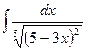
10. 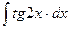
11. 
12. 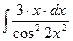
13. 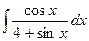
14. 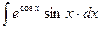
15. 
16. 
17. 
18. 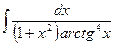
19. 
20. 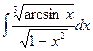
21. 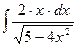
22. 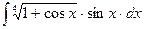
23. 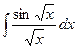
24. 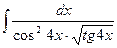
25. 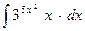
4. **Знайти невизначений інтеграл методом заміни змінної.
1) 
2) 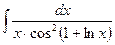
3) 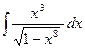
4) 
5) 
6) 
7) 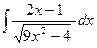
8) 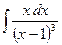
9) 
10) 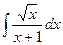
11) 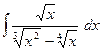
12) 
13) 
14) 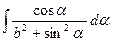
15) 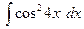
16) 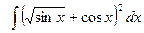
17) 
18) 
19) 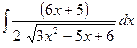
20) 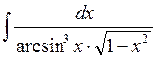
21) 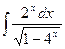
22) 
23) 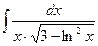
24) 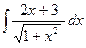
25) 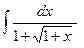
26) 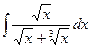
27) 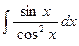
28) 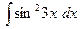
29) 
30) 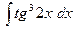
5. ***Обчислення невизначеного інтеграла
методом заміни змінної
1. 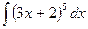
2. 
3. 
4. 
5. 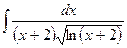
6. 
7. 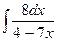
8. 
9. 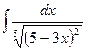
10. 
11. 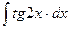
12. 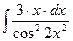
13. 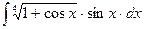
14. 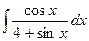
15. 
16. 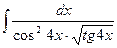
17. 
18. 
19. 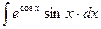
20. 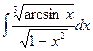
21. 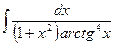
Дата добавления: 2016-06-02; просмотров: 774;
