Площі геометричних фігур.
| Фігура | Співвідношення між елементами | |||
Прямокутний трикутник
    
|  теорема Піфагора теорема Піфагора





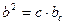
| 



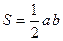
| ||
Трикутник


|  , , 
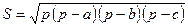 - формула Герона, - формула Герона, 
 , , 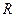 - радіус описаного кола - радіус описаного кола
 , ,  - радіус вписаного кола - радіус вписаного кола
 , ,  - для правильного трикутника. - для правильного трикутника.
| |||
Прямокутник

| 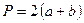
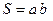

| |||
Квадрат

| 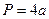

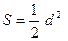
| |||
Паралелограм
     
| 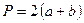

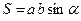
| 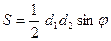

| ||
Ромб

|
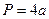

| 

| ||
Трапеція


| 
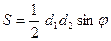
| 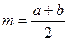 - довжина середньої лінії - довжина середньої лінії
| ||
 - довжина кола - довжина кола
|  - площа круга - площа круга
| |||
Площі поверхонь та об’єми геометричних тіл.
| Назва | Зображення | Площа поверхні | Об’єм |
| Призма |

| Sбічної=P l P- периметр l- висота бічної грані | V=Sоснови H Н- висота призми |
| Піраміда |

|
Sбічної=  P hбічної
Р – периметр основи P hбічної
Р – периметр основи
|
V=  Sоснови H Sоснови H
|
| Зрізана піраміда |

|
Sбіч=  (P1+Р2) hбіч
Р1 , Р2 – периметри основ (P1+Р2) hбіч
Р1 , Р2 – периметри основ
|
V=  (S1+ (S1+ 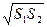 +S2) H
S1 ,S2 – площі основ +S2) H
S1 ,S2 – площі основ
|
| Циліндр |

| Sбічн=2πRH | V=πR2 H |
| Конус |

| Sбічн=πRL L - твірна |
V=  πR2 H πR2 H
|
| Зрізаний конус |

| Sбічн=π(R+r)L |
V=  π(R2+Rr+r2) H π(R2+Rr+r2) H
|
| Сфера, куля |

| S=4πR2 |
V=  πR3 πR3
|
| Кульовий сектор |

| ---- |
V=  πR2 H πR2 H
|
| Кульовий сегмент |

| S=2πRH |
V=  πH2 (3R-H) πH2 (3R-H)
|
Паралельні проекції деяких плоских фігур.
  
| проекція – трикутн ик будь – якої форми | ||||||||||||||||||||||||
| проекція –паралелограм будь – якої форми | ||||||||||||||||||||||||
  
| проекція – трапеція будь – якої форми | ||||||||||||||||||||||||
  
| проекція кола - еліпс |
7.
Дата добавления: 2016-06-02; просмотров: 844;





