Складання проекту прецизійної мережі для забезпечення облікової одиниці площі 1 кв.м.

На мал. 5.1. приведена схема тріангуляії обласного центру . На топографічній карті масштабу 1:10000 запроектована центральна система із 8 трикутників . Центральний пункт А запроектовано на даху 14 поверхового будинку з якого є добра видимість на 8 пуктів , розміщених , також , на дахах висотних будинків у різних частинах міста . Вихідний базис АВ вимірюється з точністю 1:1 000 000 . Довжина базисної сторони 2900,000 м . Координати визначаються у відносній системі координат .

Кути вимірюються транспортиром з точністю 0,5° . При цьому слідкують за тим , щоб сума кутів у трикутнику була рівною 180° , а сума кутів при центральному пункті 360° .

			F

	В

Для побудови моделі геодезичної мережі необхідно підібрати так значення кутів ,щоб виконувалися умови фігур , горизонту і полюса . Лише в цьому випадку визначені координати пунктів можна прийняти за істинні координати , а кути - за істинні значення кутів .

Виконується попереднє рішення трикутників - визначаються довжини сторін і вільний член полюсного умовного рівняння . Рішення тикутників виконується за теоремою синусів :

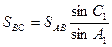, (5.5)

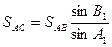, (5.6)

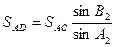, (5.7)

Підставляючи (5.6) у (5.7), отримаємо:

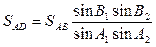. (5.8)

Діючи по аналогії , будемо мати :

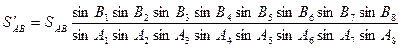
де S_АB - довжина виміряного базиса ;

S¢_ав - розрахована довжина базиса при передачі сторін .

Полюсне умовне рівняння при цьому буде :

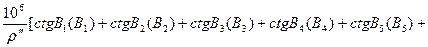
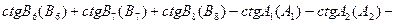(5.10)

,

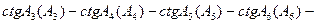
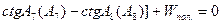де

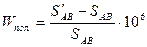, (5.11)

(B_i), (A_i) - невідомі поправки у виміряні відповідно кути В_i, А_i;

р" - число секунд в одному радіані.

Крім умовного рівняння полюса в даній мережі повинна задовольнятись умова горизонту , якщо вимірюються кути :

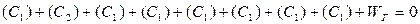(5.12)

де (С_i) - поправки в центральні кутиС_i. При цьому :

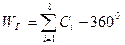. (5.13)

В даній мережі повинно задовільнятись вісім умовних рівнянь фігур : 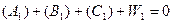(5.14)

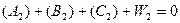(5.15)

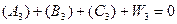(5.16)

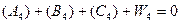(5.17)

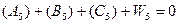(5.18)

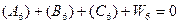(5.19)

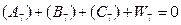(5.20)

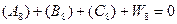(5.21)

де 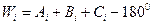. (5.18)

Поправка за умову полюса у зв'язуючі кути трикутників при спрощеному зрівноваженні знаходиться за формулою :

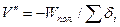, (5.23)

де 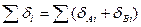, (5.24)

а 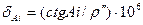(5.25)

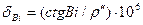(5.26)

З врахуванням всіх умовних рівнянь проводиться зрівноваження центральної системи . У зрівноваженій моделі задовольняються всі умовні рівняння .

Отримана зрівноважена система сприймається як істинна модель мережі, зрівноважені сторони - за істинні сторони , зрівноважені кути - за істинні кути .

Далі дослідження проводиться методом спотвореної моделі .При цьому генеруються випадкові похибки по тому чи іншому закону .

У наших дослідження х генеруються псевдовипадкові похибки 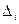, розподілені за нормальним законом :

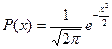(5.27)

Значення 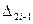, 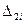. генеруються із 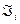(i=1,2,3...) за формулами :

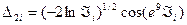(5.28)

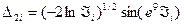(5.29)

Значення 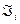. виробляються за допомогою лінійного

конгруентного методу :

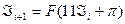, (5.30)

де Р(Z) - дробна частина від Z . Розрахунки раціонально вести на програмованому мікрокалькуляторі МК 52 .

При цьому можна задаватись будь-якою середньою квадратичною похибкою моделі польових спостережень.

Ввівши генеровані похибки у значення кутів істинної моделі, отримують спотворену модель. Генеровані похибки розглядаються як істинні похибки виміряних кутів.

Провадиться строге зрівноваження мережі корелатним способом. Використовується двогруповий спосіб зрівноваження Крюгера - Урмаєва. В першу групу відносять умовні рівняння фігур. Розподіливши нев'язку кожного трикутника порівну на кожний кут, розраховують вільні члени умовних рівнянь горизонту і полюсу за попередньо вирівняними кутами за умови фігур.

Розраховують перетворені коефіцієнти умовних рівнянь горизонту і полюсу

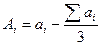
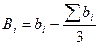
де а_i, b_i - неперетворені коефіцієнти в одному трикутнику;

А_i, В_i - перетворені коефіцієнти.

Контролем розрахунку перетворених коеффіціентів є рівність нулю суми коефіцієнтів у кожному трикутнику.

Від перетворених коефіцієнтів двох умовних рівнянь переходять до коефіцієнтів нормальних умовних рівнянь і виконують процедуру строгого зрівноваження.

Знайшовши корелати, розраховують поправки у вторинні у кути:

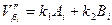
де k₁ і k₂ - координати.

Отримують зрівноважені кути шляхом додавання вторинної поправки до попередньо виправлених кутів за умови фігур.