Оцінка точності елементів запроектованої мережі.

Виконавши процедуру суворого зрівноваження спотвореної мережі, провадять порівняльний аналіз точності елементів.

З цією метоюдається розрахунок істинних координат і зрівно-важених координат. Приводиться порівняльна таблиця істинних і зрівноважених значень координат, виписуються істинні похибки зрівноважених координат, які розраховуються за формулами

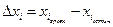
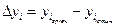
Розраховується середня квадратична похибка координат

,

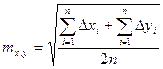де п - число пунктів, координати яких визначаємо.

Провадиться розрахунок середньої квадратичної похибки одиниці ваги

,

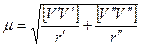де 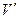, 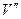- первинна і вторинна поправки в кути відповідно;

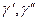- кількість умовних рівнянь першої і другої групи.

Для проведення більш детальних досліджень розраховується сумарна поправка

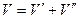(5. 36)

і середня квадратична похибка одиниці ваги за сумарною поправкою

,

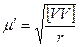де 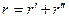. (5.38)

Приводиться розрахунок середньої квадратичної похибки моделювання кута за формулою Гаусса

,

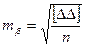де 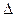- істинні значення генерованих похибок;

n - кількість генерованих похибок.

Дається розрахунок середньої квадратичної похибки моделювання кута за формулою Ферреро

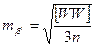
де W - нев'язки в трикутниках ( вільні члени умовних рівнянь фігур);

n - кількість трикутників.

Приводиться розрахунок середньої квадратичної похибки дирекційного кута m_aAF в найбільш слабкому місці мережі

,

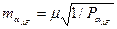де 1/Р_aAF - величина оберненої ваги, яку отримують із вирішення схеми Гаусса за попередньо складеною ваговою функцією.

У нашому випадку

F (1/ Р_aAF) = (С₁) + (С₂) + (С_з) + (С₄), (5.42)

Коефіцієнти вагових функцій також перетворюють за формулами (5.29), (5.30).

Приводиться розрахунок середньої квадратичної похибки сторони АF в найбільш слабкому місці

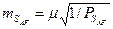
де 1/Р_aAF береться із схеми Гаусса на підставі складеної вагової функції

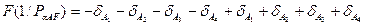(5.4.4)

Середня квадратична похибка слабкої сторони, виражена в метрах, буде

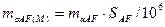(5.45)

відносна похибка

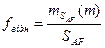
Дається порівняльна таблиця істинних і зрівноважених дирекційних кутів і сторін.