Попереднє рішення трикутників і обчислення сферичних надлишків .

Для того щоб обчислити поправки у виміряні напрямки за центрування теодоліта і редукції візирних цілей необхідно знайти спочатку довжини сторін трикутників . При цьому зразу ж обчислюють їх сферичні надлишки .

При рішенні трикутників доцільно придержуватись слідуючих рекомендацій :

-виділити на схемі мережі ланку послідовного рішення трикутників і пронумерувати їх по порядку . Трикутники , які не попали в цю ланку , нумеруються і розв'язуються останніми ;

- в кожному трикутнику на першому місці виписується номер вершини того кута , який лежить проти вихідної сторони , служить вихідною при рішенні слідуючого трикутника ;

- кути виписують округлюючи їх до 10” , причому так , щоб сума кутів в трикутнику була рівна точно ;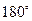

- протилежні кути і сторони трикутника записують постросно . У трикутнику з виміряними кутами А,В,С довжини протилежачих сторін обчислюють за теоремою синусів :

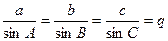(5.1)

звідки , прийнявши сторону а за вихідну , знаходять довжини других сторін :

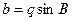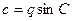, . (5.2)

Обчислення сторін трикутників починається від вихідної сторони тріагуляції . Величина q записуєтьсянад обчисляємими сторонами трикут ника . Довжина кожної сторони знаходиться шляхом множення величини q на синус протилежного кута . Довжини сторін обчислюють до цілого метра.

Сферичний надлишок трикутника зі сторонами а , b , с визначають за формулою :

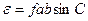, (5.3)

де сторони а , b виражають в кілометрах , а коефіцієнт :

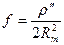, (5.4)

в якому r" = 206265, а R_m- середній радіус кривизни поверні земного еліпсоїда на широті мережі , виражений також в кілометрах . В тріангуляції 3-4 класів значення цього коефіцієнта для території бувшого Союзу приймався однаковим і рівним f=0,00253 .

Сферичні надлишки трикутників обчислюють до 0,001" в тріангуляції 1-2 класів і до 0,01" в тріангуляції 3-4 класів .