Оцінка точності елементів здвоєного ряду рівносторонніх трикутників при зрівноваженні по кутам за умови фігур , полюсів , горизонту , базисів і азимутів .
|
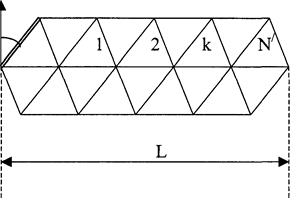
| Мал. 3.3. Здвоєний ряд тріангуляції |
На мал. 3.3. зображений здвоєний ряд тріангуляції , де b,a0
вихідна сторона і її азимут ; Sn- визначаєма сторона і її азимут a ; N' -число всіх центральних систем , які складають ряд ; к- число центральних систем , які відділяють оцінюєму сторону від вихідної ;m - середня квадратична похибка виміряного кута ;n- число трикутників , необхідне для визначення шуканої сторони .
За формулами А.В.Заводовського середня квадратична похибка логарифма сторони К-ої центральної системи :
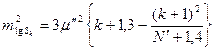 (3.13.)
(3.13.)
Відносна похибка сторони fS відн.:
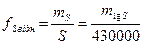 (3.14)
(3.14)
Середня квадратична похибка азимута сторони к-ої центральної системи :
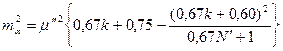 . (3.15)
. (3.15)
Середнє квадратичне значення поздовжнього зсуву :
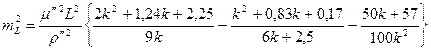 (3.16)
(3.16)
де к-число проміжних сторін , діагональ L=Sк.
Середнє квадратичне значення поперечного зсуву :
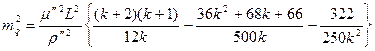 (3.17)
(3.17)
Формула (3.17.) виведена за умови зрівноваження по напрямкам . Точність передачі довжин і азимутів у подвійному ряді трикутників підвищується в порівнянні з простим рядом приблизно на ЗО % .
Дата добавления: 2016-09-20; просмотров: 563;
