Найвигідніша форма трикутників .

При дослідженні найвигіднішої форми трикутників необхідно врахувати слідуючі умови :

1) люба сторона трикутника вищого класу може бути вихідною стороною для тріангуляції нижчого класу , тому точність визначення зв'язуючої і проміжної сторін повинна бути однакова;

2) величина 1/р трикутника повинна бути найменшою ;

3) необхідно забезпечити найбільш точне визначення положення пунктів на всій території , де розвивається тріангуляція , для чого необхідно по можливості зменшувати загальне число трикутників ;

4) форма трикутників повинна сприяти нормальному розвитку ряда (мережі) в різних фізико-географічних умовах .

Перші дві умови об'єднаємо . Для того , щоб проміжна і зв'язуюча сторони n-го трикутника визначались з однаковою точністю , необхідно забезпечити рівність :

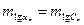, (3.6)

Середні квадратичні похибки логарифма зв'язуючої сторони а _n і проміжної сторони c_n розраховуються за формулами :

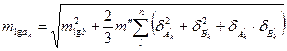, (3.7)

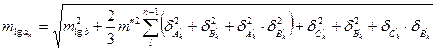(3.8)

підставляючи (3.7) , (3.8) у (3.6), отримаємо :

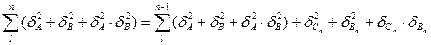
тобто

,

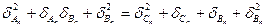звідки

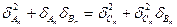(3.9)

Замінюючи в цьому рівнянні величини d їх значеннями з виразу:

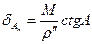, (3.10)

і поділивши ліву і праву частини рівності на 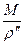, отримаємо:

.

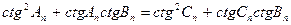Така рівність можлива, якщо:

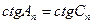
і тому

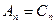(3.11)

Тобто трикутники ряду повинні бути рівнобедренними з рівними кутами при вершинах А і С . При цьому кути В в трикутниках повинні задовольняти рівності : B_k=180°-2A_k/

Величина оберненої ваги сторони для трикутника :

.

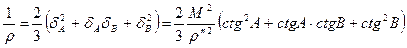Замінюючи в цій формулі кут В через 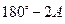, отримаємо :

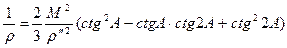(3.12)

Необхідно знайти значення кута А , при якому функція 1/р буде мінімальною .

Рішаючи цю задачу за правилами диференційного числення , знаходимо для кута А значення 52°4б'. Таким чином , якщо трикутники ряду мають кути А = 52°4б' ; С = 52°46' ; В = 74°28' , то всі їх сторони визначаються з однаковою і найменшою похибкою .

Величина 1/р для такого трикутника рівна 2,5 одиниці шостого знаку логарифма.

Третя умова зменшення загального числа трикутників краще всього виконується при рівностронніх трикутниках , тому що при одномо і тому ж периметрі вони мають найбільшу площу в порівнянні з трикутниками любої другої форми . Величина 1/р для рівностороннього трикутника рівна 2,9 одиниці шостого знаку логарифму .

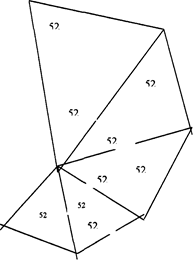
Розглянемо тепер останню умову . Рельєф місцевості часто створює труднощі для нормального прокладення тріангуляції в потрібному напрямку . Тому фактичні трикутники в загальному випадку не будуть задовольняти оптимальним умовам , але в сукупності доцільно підібрані трикутники можуть дозволити розвинути мережу з найменшим збільшенням величини 1/р і з більшими перевагами по відношенню до місцерозташування пунктів , висоти сигналів і збереження загального напрямку тріангуляції.

3. Так , як різниця у величинах 1/р незначна , то без врахування особливостей рельєфу слід признати найбільш вигідним рівносторонній трикутник.

4. В конкретних умовах виробництва слід брати до уваги не один , а групу суміжних трикутників .

5. Згідно Інструкції про побудову державної геодезичної мережі, кути в трикутниках тріангуляції 1 класу повинні бути не менші 40°, в геодезичних чотирикутниках і центральних системах - не менше 30°, а мережах тріангуляції 2-4 класів в окремих випадках допускається величина кута 20° .