Оцінка точності рядів суцільних мереж тріангуляції.
Оцінка точності елементів суцільної мережі тріангуляції, побудованої із рівносторонніх трикутників при зріввноваженні по кутам за умови фігур , горизонтів і полюса ( вільних мереж ) виконують за формулами К.П.Проворова.
Для ряду тріангуляції, виділеного із мережі з N трикутниками між вихідними сторонами ( з вихідними базисами і азимутами ) і п трикутниками від вихідної сторони до визначаємо'!', середня квадратична похибка логарифма сторони :
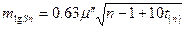, (3.1)
середня квадратична похибка азимута сторони:
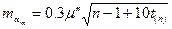, (3.2) В цих формулах t(n) =(1/2)n/2- (1/2)n+1для зручності підрахунків
величини t(n) тубальовані.
Таблиця 3.1
| n | t(n) | n | t(n) | |
| 0,457 | 0,022 | |||
| 0,375 | 0,016 | |||
| 0,291 | 0,011 | |||
| 0,219 | 0,008 | |||
| 0,161 | 0,006 | |||
| 0,117 | 0,004 | |||
| 0,084 | 0,003 | |||
| 0,060 | 0,002 | |||
| 0,043 | 0,002 | |||
| 0,031 | 0,001 |
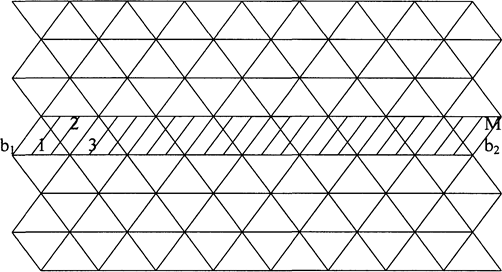
Мал 3.1. Суцільна мережа тріангуляції. Середні квадратичні значення поздовжніх і поперечних зсувів :
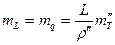, (3.3)
де L - діагональ виділеного із мережі ряду трикутників
mT -середня квадратична похибка азимута діагоналі вибраного ряду , рівна:
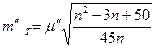, (3.4)
Сумарна похибка і положення пункту буде :
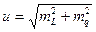, (3.5)
Дата добавления: 2016-09-20; просмотров: 496;