Оцінка точності елементів ланки полігонометрії 1 класу .

Приймаємо , що полігонометричний хід 1 класу є витягнутим , на його кінцях визначені азимути Лапласа і що він зрівноважений за умови азимутів (дирекційних кутів ).

Середня квадратична похибка азимута любої сторони ланки обчислюється за формулою :

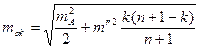, (4.17)

Поздовжній і поперечний зсуви кінцевої точки ланки відносно початкової рівні :

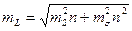, (4.18)

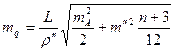, (4.19)

де п - число всіх сторін в ланці полігонометрії ;

к - номер сторони ланки ;

L = nS - довжина діагоналі ланки ;

т";т_S;т_A. - відповідно середні квадратичні похибки вимірювання кутів, довжин сторін і азимутів Лапласа ;

m_s - систематична похибка вимірювання віддалей світловіддалеміром через неточне значення швидкості поширення світла в атмосфері

(m_s»S-10^-6).

Так для L=176км; S=22км; n=8; k=4;

т"=0,7"; m_S : S = 1:300000 ; т_s=S× 10^-6 ; т_A = 1,1'' , Отримаємо :

m_ak=1,3''; т_L =0,27м; m_q=0,88 м; т_L:L =1:652000; 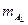=1,0''; М=0,92м.

Критерії витягнутості полігонометричного ходу :

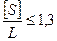(4.20)

віддаль h'₀ від вершини ходу до лінії , поведеної через центр ваги паралельно замикаючої ходу :

гран.h'₀= 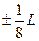, (4.21)

відхилення сторін ходу від напрямку замикаючої :

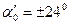. (4.22)

Висновки.

В рядах і мережах трилатерації поперечні зсуви у декілька раз більше поздовжніх ; це веде до неоднорідності похибок ряду і пред'являє підвищені вимоги до розрахунку необхідної частоти вихідних азимутів . У

цьому відношенні ряди і мережі тріагуляції вигідно відрізняються від рядів і мереж тилатерації.

Від того наскільки надійно буде встановлено -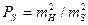

відношення квадратів похибок кутових і лінійних вимірів , залежить достовірність результатів зрівноваження мережі. Тому питанню надійного визначення величини середніх квадратичних похибок m напр. і m_s в лінійно-кутовій мережі повинна бути приділена сама серйозна увага як на стадії проектування мережі, так і на стадії постановки і виконання кутових і лінійних вимірів у ній .

Контрольні запитання.

1. Привести формули визначення точності кутів у трикутнику трилатерації.

2. Дати обгрунтування формули середньої квадратичної похибки азимута зв'язуючої сторони ряду трилатерації .

3. Дати обгрунтування формули поздовжнього зсуву ряду трилатерації.

4. Дати обгрунтування формули поперечного зсуву ряду трилатерації.

5. Обгрунтувати формули оцінки точності елементів суцільної мережі трилатерації.

6. Обгрунтувати формули оцінки точності елементів лінійно-кутового ряду .

7. Обгрунтувати формули оцінки точності елементів ланки полігонометрії 1 класу.

Лекція 5 . Попередні обчислення в планових геодезичних мережах.

План лекції.

5.1. Задачі попередніх обчислень .

5.2. Попереднє рішення трикутників і обчислення сферичних надлишків .

5.3. Складання проекту прецизійної мережі для забезпечення облікової одиниці площі 1 кв.м.

5.4. Оцінка точності елементів мережі. 5.5. Дослідження необхідної точності визначення координат пункту

Викладення матеріалу .