Розв’язання систем лінійних рівнянь за формулами Крамера
Для системи n лінійних рівнянь з n невідомими (над довільним полем)
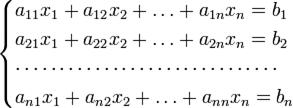
з визначником матриці системи Δ, що не рівний нулеві, розв'язок записується у такому вигляді:
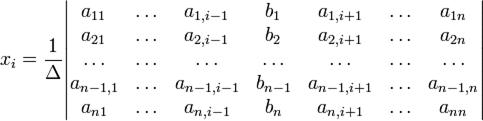
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).
Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:
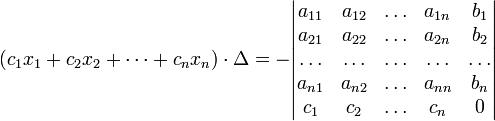
У такій формі формула Крамера справедлива без припущення, що Δ не рівне нулю.
Приклад:
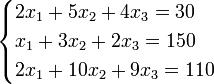
Визначники:
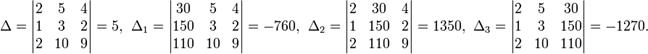
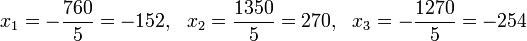
5. Приклади для розв’язування.
І. Визначте координати векторів:
1. 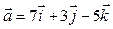 2.
2. 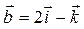
3. 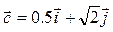 4.
4. 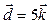
5. 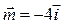 6.
6. 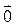
2. Відомі координати точок
А(4; -3; 2), В(-2; 4; -3), М(0; 5; 1) та N(-4; 0; -3). Знайдіть координати векторів, 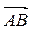 ,
, 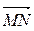 , їх модулі та косинус кута між ними.
, їх модулі та косинус кута між ними.
3. Відомі координати векторів 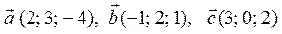 . Знайдіть координати та модулі векторів:
. Знайдіть координати та модулі векторів:
1. 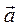 +
+ 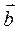 ;
;
2. 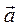 +
+ 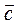 ;
;
3. 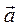 +
+ 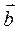 -
- 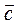 ;
;
4. 3 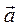 ;
;
5. - 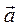 +2
+2 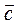 ;
;
6. 2 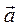 +3
+3 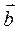 - 2
- 2 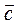 ;
;
4. Користуючись умовою колінеарності двох векторів, перевірте, чи колінеарні вектори:
1. 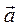 (2/5; -1/3; 4/5) та
(2/5; -1/3; 4/5) та 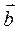 (3/5; - 1/2; 6/5)
(3/5; - 1/2; 6/5)
2. 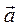 (-6; 1/3; 3) та
(-6; 1/3; 3) та 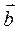 (-2; 1/9; -1/3)
(-2; 1/9; -1/3)
5. За яких значень n та p вектори 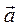 та
та 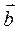 будуть колінеарними?
будуть колінеарними?
1. 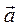 (-3; n; 4) та
(-3; n; 4) та 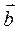 (-2; 4; р)
(-2; 4; р)
2. 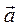 (4; n; -4) та
(4; n; -4) та 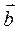 (р; -2; 1/2 )
(р; -2; 1/2 )
6. Знайдіть периметр трикутника, вершини якого задані координатами
А(8; 0; 6), В(8; -4; 6), С(6; -2; 5). Визначте вид трикутника.
7. Відрізок АВ заданий координатами кінців А(4; 2; -3) та В(6; -4; -1). Знайдіть координати точки С, яка ділить відрізок:
1. навпіл;
2. у співвідношенні 1:3;
3. у співвідношенні 2:5;
8. Доведіть, що чотирикутник з вершинами А(1; 4; 3), В(2; 3; 5), С(2; 5; 1) та D(3; 4; 3) – паралелограм.
10. Обчислити кути нахилу до осі Ох прямих:  ,
, 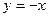 ,
, 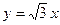 .
.
11. Скласти рівняння прямої,яка проходить через початок координат, якщо кутовий коефіцієнт дорівнює 1; 2: -1: 4.
12. Скласти рівняння прямої, яка проходить через початок координат і утворює з віссю Ох кут: 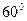 ,
, 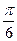 ,
, 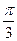 .
.
13. Знайти кутові коефіцієнти прямих, заданих рівняннями: 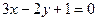 ,
, 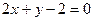 ,
, 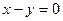 .
.
14. Скласти рівняння прямої, яка проходить через точку А і перпендикулярна вектору 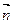 :
:
a. 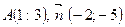
b. 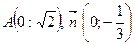
c. 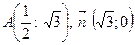
15. Скласти рівняння прямої, яка перетинає вісь Ох в точці 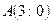 , а вісь Оу – в точці
, а вісь Оу – в точці 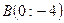 .
.
16. Обчислити площу трикутника, який відтинається прямою 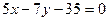 від координатного кута.
від координатного кута.
17. При якому значенні 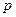 задані прямі паралельні і перпендикулярні:
задані прямі паралельні і перпендикулярні:
a. 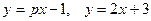
b. 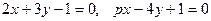

18. Дано 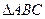 . Знайти:
. Знайти:
a. рівняння сторін;
b. довжини сторін;
c. рівняння медіани АМ;
d. довжину медіани АМ;
e. рівняння висоти 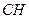 ;
;
f. точку перетину медіани АМ і висоти 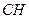 ;
;
g. 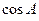 ;
;
h. зробити малюнок.
1. 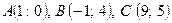
2. 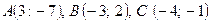
3. 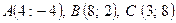
4. 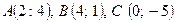
9. Розв’язування систем лінійних рівнянь за формулами Крамера та методом Гауса.
1. 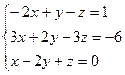 2.
2. 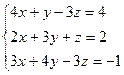 3.
3. 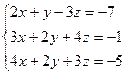
4. 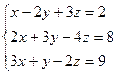 5.
5. 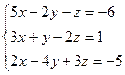 6.
6. 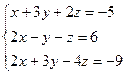
7. 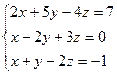 8.
8. 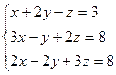 9.
9. 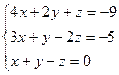
Дата добавления: 2016-06-02; просмотров: 1079;
