Поняття диференціала і його властивості.

Розглянемо диференційовану на інтервалі (a,b) функцію 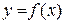. Її похідна в деякій точці х з інтервалу (a,b) визначається рівністю

.

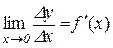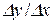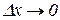Згідно з теоремою 3.1 відношення при можна подати у вигляді

,

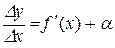де 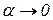при 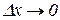. Помножимо останню рівність на :

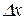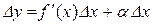. (9.1)

В загальному випадку 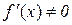, тому при сталому х і змінному 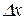, такому що 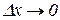, добуток 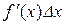є нескінченно малою величиною першого порядку відносно 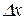. А добуток 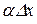є нескінченно малою величиною більш високого порядку відносно 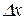, тому що

.

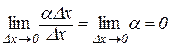Таким чином, приріст 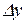функції 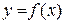складається з двох доданків, перший з яких, лінійний відносно 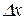називається головноючастиноюприросту.

Означення 9.1. Головна частина приросту 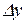функції 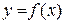, тобто 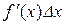, називається диференціалом функції 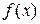і позначається 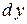або .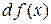

Таким чином згідно з означенням

.

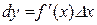Для визначення змісту диференціала аргументу х знайдемо диференціал функції у=х:

.

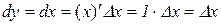Отже, диференціал 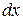аргументу х рівний його приросту 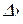, тобто 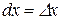. Диференціал функції тепер можна записати у вигляді

.

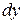
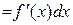З останньої рівності можна отримати ще одне позначення для похідної:

.

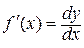Тобто похідну можна розглядати як відношення диференціала функції до диференціала аргументу.

Приклад 9.1. Знайти диференціал функції .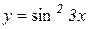

Розв’язування:

.

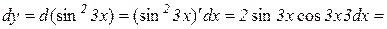
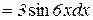Відшукання диференціала рівносильне обчисленню похідної, оскільки, помноживши останню на диференціал аргументу, дістанемо диференціал функції. Тому більшість властивостей і формул, справедливих для похідної, справджуються й для диференціала.