Властивості диференціала.
Якщо 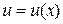 і
і 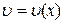 – диференційовані функції, то:
– диференційовані функції, то:
1. 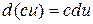 , де
, де 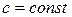 .
.
2. 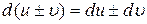 .
.
3. 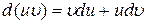 .
.
4. 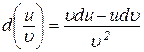 .
.
5. Якщо 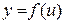 , де
, де 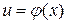 , то
, то 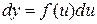 . Тобто диференціал складної функції має такий вигляд, якого б він отримав при незалежному проміжному аргументу u.
. Тобто диференціал складної функції має такий вигляд, якого б він отримав при незалежному проміжному аргументу u.
Доведення Вл. 4. З означення диференціала маємо
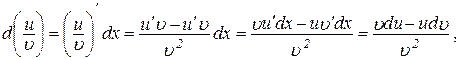 ,
,
так як 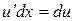 і
і 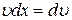 .
.
Доведення Вл. 5. Дійсно, з означення диференціала
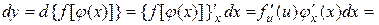
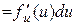 ,
,
так як 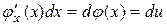 .
.
Приклад 9.2. Знайти диференціал функції 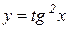 .
.
Розв’язування. Запишемо дану функцію у вигляді 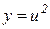 , де
, де 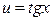 . Тоді
. Тоді
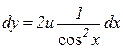 або
або 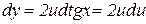 ,
,
тобто 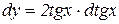 .
.
9.2.Застосування диференціала для наближених
Обчислень.
З рівності (9.1) і означення диференціала маємо 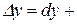
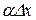 , тому приріст функції
, тому приріст функції 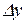 з точністю до числа
з точністю до числа 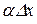 можна замінити диференціалом
можна замінити диференціалом 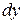 , тобто
, тобто 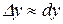 . Причому остання рівність буде тим точнішою, чим менше
. Причому остання рівність буде тим точнішою, чим менше 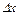 . Перепишемо її у вигляді
. Перепишемо її у вигляді
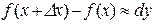
або
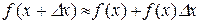 . (9.2)
. (9.2)
Покаже на прикладі, як за допомогою формули (9.2) можна проводити наближені обчислення.
Приклад 9.3. Обчислити 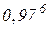 .
.
Розв’язування. Запишемо рівність (9.2) у вигляді
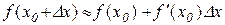 .
.
В нашому прикладі 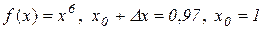 ,
, 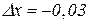 . Знайдемо
. Знайдемо 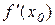 :
:
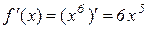 ;
;
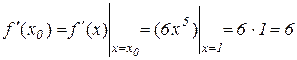 .
.
Таким чином,
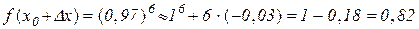 .
.
9.3. Похідні вищих порядків.
Розглянемо диференційовану на деякому інтервалі 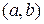 функцію
функцію 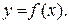 . Похідна
. Похідна 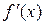 , взагалі кажучи, залежить від змінної х, тобто є новою функцією аргументу х, для якої можна ставити питання про обчислення похідної.
, взагалі кажучи, залежить від змінної х, тобто є новою функцією аргументу х, для якої можна ставити питання про обчислення похідної.
Означення 9.2. Похідна від першої похідної називається похідною другого порядку або другою похідною від початкової функції і позначається 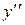 або
або 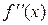 .
.
Згідно з означенням 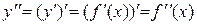 .
.
В свою чергу друга похідна 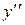 також є функцією аргументу х і її можна диференціювати.
також є функцією аргументу х і її можна диференціювати.
Похідна від другої похідної називається похідною третього порядку або третьою похідною і позначається 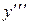 або
або 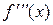 .
.
Аналогічно вводиться похідна будь-якого порядку: похідна від похідної 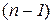 -го порядку називається похідною n-го порядку або n-ю похідною і позначається
-го порядку називається похідною n-го порядку або n-ю похідною і позначається 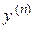 або
або 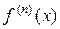 . Таким чином
. Таким чином
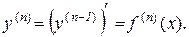 .
.
Похідні позначаються римськими цифрами або взятими в дужки арабськими, щоб розрізняти з показником степеня.
Приклад 9.4. Знайти похідну четвертого порядку для функції
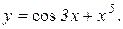 .
.
Розв’язування.
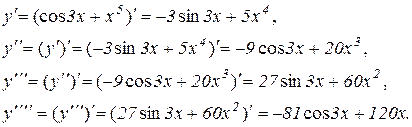
9.4.Диференціали вищих порядків.
Нехай функція 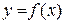 диференційована на деякому інтервалі
диференційована на деякому інтервалі 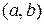 . Її диференціал
. Її диференціал 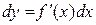 є деякою функцією аргументу х. Але від х залежить тільки множник
є деякою функцією аргументу х. Але від х залежить тільки множник 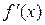 , а диференціал
, а диференціал 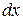 є приростом аргументу і від значення х не залежить. Таким чином, можна ставити питання про обчислення диференціала від функції
є приростом аргументу і від значення х не залежить. Таким чином, можна ставити питання про обчислення диференціала від функції 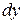 .
.
Означення 9.3. Диференціал від диференціала функції 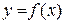 називається другим диференціалом або диференціалом другого порядку цієї функції і позначається
називається другим диференціалом або диференціалом другого порядку цієї функції і позначається 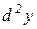 або
або 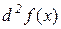 .
.
З означення диференціала випливає, що:
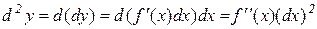 .
.
Величина 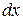 не залежить від х і ми винесли її за знак похідної. Замість
не залежить від х і ми винесли її за знак похідної. Замість 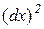 прийнято писати
прийнято писати 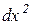 , розуміючи під цим не
, розуміючи під цим не 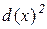 , а
, а 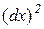 .
.
Диференціал від другого диференціала називається третімдиференціалом або диференціаломтретьогопорядку і позначається 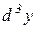 або
або 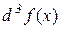 . Аналогічно другому диференціалу отримаємо
. Аналогічно другому диференціалу отримаємо
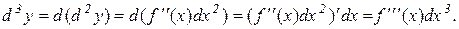
Диференціалом n-гопорядку або n-м диференціалом називається диференціал від (n-1)-го диференціала:
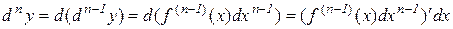
або
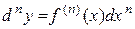 .
.
За допомогою диференціалів різних порядків можна виразити відповідні похідні:
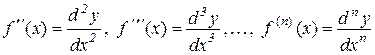 .
.
Приклад 9.5. Знайти диференціал третього порядку для функції
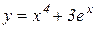 .
.
Розв’язування. З означення третього диференціала маємо
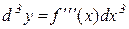 .
.
Знайдемо 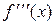 :
:
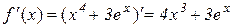 ,
,
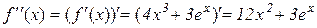 ,
,
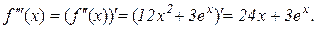
Таким чином, 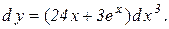
9.5. Похідна другого порядку функції, заданої
Дата добавления: 2016-05-05; просмотров: 3431;
