Допомогою другої похідної.

Теорема 11.5. Нехай 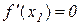і друга похідна 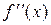неперервна в деякому околі точки х₁ , тоді при 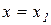функція має максимум, якщо , і – мінімум, якщо .

Доведення. Доведемо першу частину теореми. Нехай 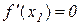і 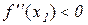. З неперервності функції 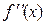в деякому околі точки х₁ випливає, що можна знайти відрізок 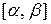, якому належить точка х₁ і в якому виконуватиметься умова .

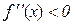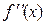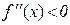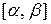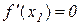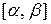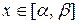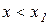Оскільки – перша похідна функції , то з умови виходить, що спадає на відрізку . Але і функція неперервна на , тому що неперервна її похідна. Отже, для має місце , коли , і 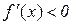, коли 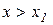. Таким чином, похідна під час переходу зліва направо через точку х₁ змінює свій знак з “+” на “–”, а це означає (див. теорему 11.4), що в точці х₁ функція 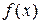набуває максимуму.

Аналогічно доводиться друга частина теореми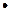

Зауваження 11.1. Якщо в критичній точці х₁ друга похідна дорівнює нулю, тобто 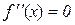, то дана теорема не дає відповіді на запитання про існування екстремуму в точці х₁ , і дослідження потрібно проводити за допомогою теореми 11.4.

Теорема 11.5 в деяких випадках спрощує дослідження функції на екстремум: в п. 4) приведеної на початку параграфа схеми треба знайти тільки другу похідну і її знак у критичній точці.

Приклад 11.6. Дослідити на екстремум функцію

.

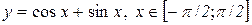Розв’язування. Функція визначена на всій числовій прямій. Знаходимо першу й другу похідну:

.

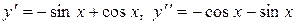Шукаємо критичні точки функції:

.

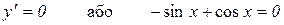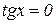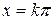Звідси або , де

Відрізку 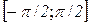належить тільки одна критична точка . Знайдемо значення другої похідної при :

.

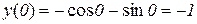Таким чином, на відрізку 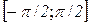функція має тільки один екстремум, а саме, максимум:

.

11.7. Найбільше та найменше значення функції

на відрізку.

Якщо функція 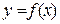неперервна на відрізку 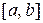, то на цьому відрізку вона досягає свого найменшого і найбільшого значень (див. теорему 5.2). Очевидно (див. рис. 11.4), що неперервна функція може набувати своїх найменших та найбільших значень у точках екстремуму або на кінцях відрізка, що розглядається. Тому для відшукання найбільшого та найменшого значень функції на відрізку можна запропонувати таку схему:

1. знаходимо екстремуми функції на заданому відрізку;

2. знаходимо значення функції на кінцях відрізка;

3. із здобутої множини значень функції вибираємо її найменше і найбільше значення.

Приклад 11.7. Знайти найменше і найбільше значення функції на відрізку .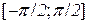

Розв’язання. 1) Знаходимо екстремуми функції:

а) ;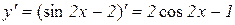

б) критичні точки функції:

.

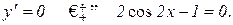Отримаємо

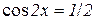
або

.

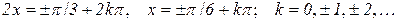Відрізку 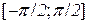належать тільки дві критичні точки 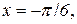, 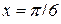. Знаходимо значення функції в цих точках:

,

.

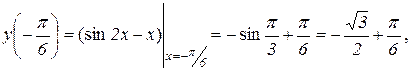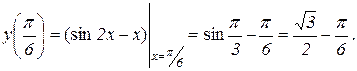2) Обчислимо значення функції на кінцях відрізка:

,

.

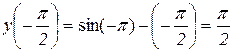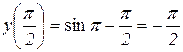3) Таким чином,

,

.

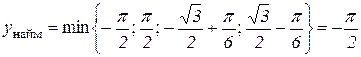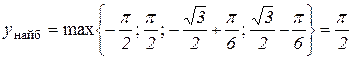11.8.Застосування теорії екстремумів до