розв’язування задач.
За допомогою теорії екстремумів розв’язується багато задач з геометрії, механіки тощо. Наведемо кілька прикладів.
Приклад 11.8. Побудувати рівнобедрену трапецію, яка при даній площі S і даному куті при основі 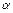 мала б найменший периметр.
мала б найменший периметр.
Розв’язання. Нехай 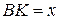 (рис. 11.9). Тоді з формули для площі трапеції
(рис. 11.9). Тоді з формули для площі трапеції
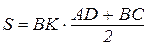 ,
,
де 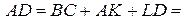
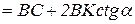 ,
,
виразимо верхню основу BC через площу S і висоту ВК:
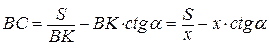 .
.
Периметр трапеції:
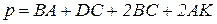
приводиться до вигляд
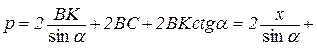
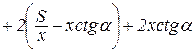 ,
,
або
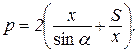 .
.
Дослідимо функцію 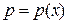 на мінімум:
на мінімум:
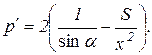 .
.
Знаходимо критичні точки функції
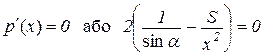 .
.
Звідси дістаємо 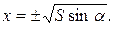 . Задача має зміст при
. Задача має зміст при 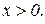 .
.
Оскільки при 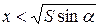 похідна
похідна 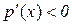 , а при
, а при 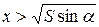 –
– 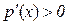 , то в точці
, то в точці 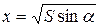 функція
функція 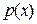 набуває мінімуму.
набуває мінімуму.
Таким чином, мінімальний периметр матиме трапеція з висотою, що дорівнює 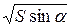 .
.
Приклад 11.9. Витрати на паливо для пароплава пропорційні кубу його швидкості. Відомо, що при швидкості 10 км/год витрати на паливо становлять 30 крб. за годину, решта витрат (незалежних від швидкості) становлять 480 крб. за годину. За якої швидкості пароплава загальна сума витрат на 1 км шляху буде найменшою? Яка при цьому буде загальна сума витрат на годину?
Розв’язання. Нехай х – швидкість пароплава; z – загальна сума витрат на рух пароплава за одну годину. Остання сума складається з витрат на паливо 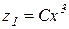 (залежних від швидкості) і з витрат
(залежних від швидкості) і з витрат 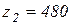 (незалежних від швидкості), тобто
(незалежних від швидкості), тобто 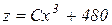 .
.
Коефіцієнт пропорційності С знайдемо з умови
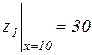 .
.
Маємо 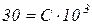 або
або 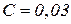 .
.
Один кілометр пароплав проходить за час 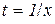 , а витрати за цей час становлять
, а витрати за цей час становлять 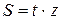 або
або 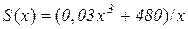 .
.
Дослідимо функцію 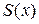 на мінімум:
на мінімум:
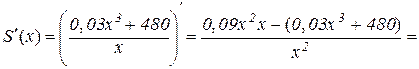
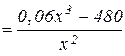 .
.
Знаходимо критичні точки:
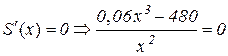
або
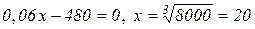 .
.
Оскільки 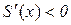 при
при 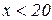 , і
, і 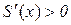 при
при 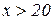 , то в точці
, то в точці 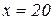 функція
функція 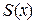 має мінімум.
має мінімум.
Таким чином, при швидкості 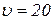 км/год загальна сума витрат на один кілометр шляху буде найменшою. Зо одну годину при цьому витрачатиметься
км/год загальна сума витрат на один кілометр шляху буде найменшою. Зо одну годину при цьому витрачатиметься 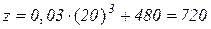 крб.
крб.
Запитання для самоконтролю.
1. Сформулюйте необхідну і достатню умову зростання функції.
2. Який геометричний зміст указаних умов?
3. Дайте означення максимуму і мінімуму функції.
4. Що таке екстремум функції? Чи може він досягатися на кінцях відрізка?
5. Сформулюйте і доведіть необхідну умову існування екстремуму функції.
6. Який геометричний зміст умови в попередньому запитанні?
7. Чи в усіх точках, де 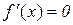 , існує екстремум функції
, існує екстремум функції 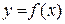 ?
?
8. Дайте означення критичної точки функції.
9. Сформулюйте і доведіть достатню умову існування екстремуму функції.
10. Наведіть схему дослідження функції на екстремум за допомогою першої похідної.
11. Як за допомогою другої похідної можна дослідити функцію на екстремум?
12. Наведіть схему дослідження функції на найбільше і найменше значення функції
13. Наведіть приклади застосування теорії екстремумів для розв’язування задач.
Приклади до розділу 11.
1. Знайти інтервали монотонності функції:
а) 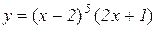 .
.
Відп.: 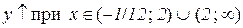 ,
,
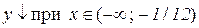 .
.
б) 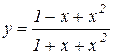 . Відп.:
. Відп.: 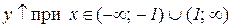 ,
,
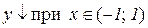 .
.
в) 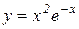 . Відп.:
. Відп.: 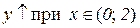 ,
,
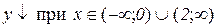 .
.
г) 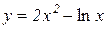 . Відп.:
. Відп.: 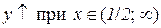 ,
,
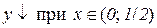 .
.
2. Знайти екстремуми функції:
а) 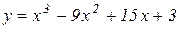 . Відп.:
. Відп.: 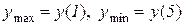 .
.
б) 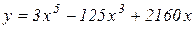 . Відп.:
. Відп.: 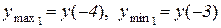 ,
,
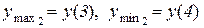 .
.
в) 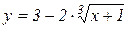 . Відп.: Не існує ні
. Відп.: Не існує ні 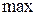 , ні
, ні 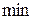 .
.
г) 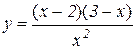 . Відп.:
. Відп.: 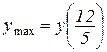 .
.
д) 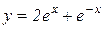 . Відп.:
. Відп.: 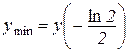 .
.
е) 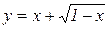 . Відп.:
. Відп.: 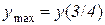 .
.
3. Знайти найменше і найбільше значення функції на вказаних відрізках:
а) 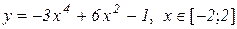 . Відп.:
. Відп.: 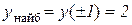 ,
,
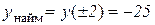 .
.
б) 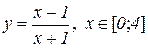 . Відп.:
. Відп.: 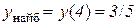 ,
,
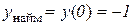 .
.
4. Розбити число 36 на два множники таких, щоб сума їх квадратів була найбільшою. Відп.: 6 і 6.
5. Знайти висоту конуса найбільшого об’єму, який можна вписати в кулю радіуса R . Відп.: 4R/3.
6. З листка, який має форму круга радіуса R, вирізати сектор, з якого можна зробити конічну фігуру найбільшої ємності.
Відп.: 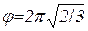 .
.
7. Потрібно вирити силосну яму об’ємом 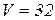 м3 з квадратним дном. Якими мають бути розміри ями, щоб на облицювання пішла мінімальна кількість матеріалу?
м3 з квадратним дном. Якими мають бути розміри ями, щоб на облицювання пішла мінімальна кількість матеріалу?
8. Швидкість у зростання популяції х задається формулою 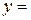
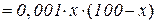 . Знайти розміри популяції, за яких ця швидкість максимальна? Яка популяція є врівноваженою, тобто для якої популяції швидкість зростання дорівнює нулю?
. Знайти розміри популяції, за яких ця швидкість максимальна? Яка популяція є врівноваженою, тобто для якої популяції швидкість зростання дорівнює нулю?
10. Залежність між урожаєм у (ц/га) озимої пшениці і нормою висіву насіння х (млн. зерен) виражається функцією
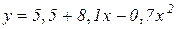 .
.
Знайти оптимальну норму висіву насіння, щоб одержати максимальний урожай.
Дата добавления: 2016-05-05; просмотров: 629;
