В теории двойственности важное значение имеют две теоремы, определяющие связь между решениями прямой и двойственной задач.
Теорема двойственности. Если из пары двойственных задач одна имеет оптимальный план, то и вторая тоже имеет оптимальный план, причем оптимальные значения целевых функций обеих задач равны между собой:
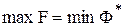 .
.
При этом 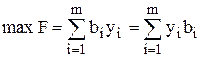 . Отсюда следует, что двойственная переменная yi является коэффициентом при bi и, следовательно, показывает, как изменится целевая функция при изменении i- го ресурса на единицу. В литературе двойственные переменные часто называют двойственными оценками.
. Отсюда следует, что двойственная переменная yi является коэффициентом при bi и, следовательно, показывает, как изменится целевая функция при изменении i- го ресурса на единицу. В литературе двойственные переменные часто называют двойственными оценками.
Теорема равновесия. План 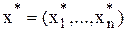 прямой задачи и план
прямой задачи и план 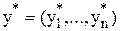 соответствующей двойственной задачи являются оптимальными при выполнении следующих условий:
соответствующей двойственной задачи являются оптимальными при выполнении следующих условий:
- если при подстановке компонент оптимального плана 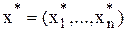 в систему ограничений исходной задачи i-е ограничение обращается в неравенство, то i-я компонента оптимального плана двойственной задачи
в систему ограничений исходной задачи i-е ограничение обращается в неравенство, то i-я компонента оптимального плана двойственной задачи 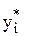 равна нулю.
равна нулю.
- если i-я компонента оптимального плана двойственной задачи 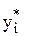 положительна, то i-е ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.
положительна, то i-е ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.
Таким образом, в парах соотношений
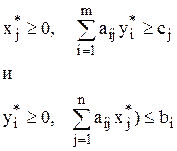
из знака строгого неравенства во одном соотношении каждой пары следует знак строгого равенства в другом.
Условия теоремы равновесия часто записывают в виде
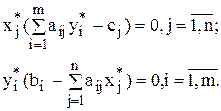
и называют условиями дополняющей нежесткости.
Из рассмотренных теорем можно сделать следующие выводы:
А) Всякий раз, когда i-е ограничение прямой задачи обращается в строгое неравенство, i-я компонента решения двойственной задачи обращается в 0.
Аналогично, всякий раз, когда i-е ограничение двойственной задачи выполняется как строгое неравенство, j-ая компонента оптимального плана обращается в ноль.
Б) Обратно, если i-я компонента оптимального плана двойственной задачи положительна, i-е ограничение исходной задачи выполняется как строгое равенство. Верно и для двойственной задачи.
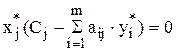
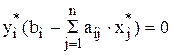
Отсюда следует:
а) Если двойственная оценка yi* = 0, то сырье i-го вида не полностью используется при производстве продукции.
б) Если j-е ограничение двойственной задачи выполняется как строгое неравенство, то j-ый вид продукции выпускать экономически нецелесообразно, хj =0 (т.е. в двойственной задаче цена всех ресурсов больше прибыли)
в) Если yi ¹ 0, то сырье i-го типа полностью используется при производстве.
Значения двойственных оценок можно определить по симплексной таблице решения прямой задачи следующим образом: -( ), где j-номера столбцов единичных векторов из исходной симплекс-таблицы (на начальной итерации); -окончательные оценки из последней симплекс-таблицы, соответствующие этим векторам. При этом индексы двойственных оценок определяются номером ограничения, которому они соответствуют.
Необходимо заметить, что если в качестве канонической формы рассматривается задача максимизации, то сумма 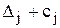 берется без знака “-“.
берется без знака “-“.
Двойственный симплекс-метод
Пусть необходимо решить задачу линейного программирования, записанную в канонической форме
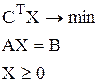
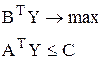
Рассмотрим начальную симплекс-таблицу этой задачи. Очевидно, что в ее столбцах записана прямая задача, а в строках — двойственная. Оценками плана исходной задачи является — сj, а оценками плана двойственной задачи bi.
Решим двойственную задачу по симплекс-таблице исходной задачи. Найдем решение двойственной задачи, а вместе с ним опорный план исходной задачи. Этот метод называется двойственным симплекс-методом.
Особенностью двойственного симплекс-метода является то, что его можно применять при решении задач линейного программирования. правые части ограничений которых являются отрицательными числами.
Алгоритм двойственного симплекс-метода.
1. 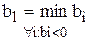 (выбор ведущей строки l)
(выбор ведущей строки l)
2. Если в ведущей строке l 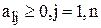 , то исходная задача не имеет решения. Если есть
, то исходная задача не имеет решения. Если есть 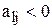 , то выбирается ведущий столбец.
, то выбирается ведущий столбец.
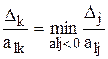 - если исходная задача на максимум, то ‘-‘.
- если исходная задача на максимум, то ‘-‘.
3. Пересчет элементов c-таблицы осуществляется по правилу симплекс метода.
4. 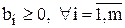 - признак оптимальности решения(когда все правые части неотрицательны)
- признак оптимальности решения(когда все правые части неотрицательны)
Задачи дробно-линейного программирования
Общая задача дробно-линейного программирования состоит в определении максимального (минимального) значения функции
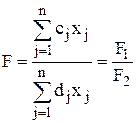
при условиях
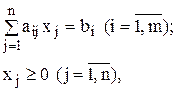
где cj, dj, bi и aij– постоянные числа, 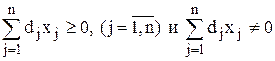 в области неотрицательных решений системы линейных уравнений, задающих ограничения. Предположение, что
в области неотрицательных решений системы линейных уравнений, задающих ограничения. Предположение, что 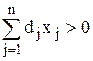 не нарушает общности задачи, поскольку в том случае, когда эта величина отрицательна, минус можно отнести к числителю.
не нарушает общности задачи, поскольку в том случае, когда эта величина отрицательна, минус можно отнести к числителю.
Сформулированная задача может быть сведена к задаче линейного программирования. Для этого следует обозначить
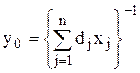
и ввести новые переменные
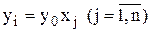 .
.
Используя введенные обозначения, исходную задачу сведем к следующей - найти максимум (минимум) функции
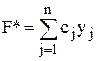
при условиях
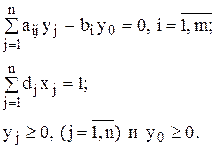
Построенная задача является задачей линейного программирования, следовательно, ее решение можно найти известными методами. Зная оптимальный план этой задачи, на основе соотношений 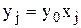 , получаем оптимальный план исходной задачи.
, получаем оптимальный план исходной задачи.
Пример . Для производства двух видов изделий A и В используются два типа технологического оборудования. Первое изделие проходит обработку только на втором типе оборудования, второе - на первом и на втором. Время обработки каждого из изделий на оборудовании данного типа приведено в табл. 9. Там же указаны затраты, связанные с производством одного изделия каждого вида.
Таблица 9
| Тип оборудования | Затраты времени (ч) на обработку одного изделия | |
| A | B | |
| I | ||
| II | ||
| Затраты на производство Одного изделия |
Оборудование II типа предприятие может использовать не более 52 часов. При этом оборудование I типа целесообразно использовать не менее 16 часов. Требуется определить, сколько изделий каждого вида следует изготовить, чтобы себестоимость одного изделия была минимальной.
Составим математическую модель задачи. За x1 обозначим количество выпускаемых изделий вида A, за x2 – количество изделий вида B. Себестоимость определяется следующим образом: С=З/K, где К – количество выпускаемых изделий, З - общие затраты на их производство. Тогда получим следующую задачу дробно-линейного программирования:
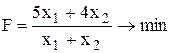 ;
;
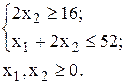
Преобразуем ограничения-неравенства данной задачи в равенства:
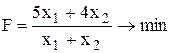 ;
;
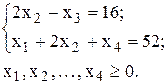
Сведем данную задачу к задаче линейного программирования. Для этого обозначим 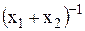 через y0 и введем новые переменные
через y0 и введем новые переменные 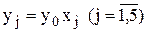 .
.
В результате приходим к следующей задаче: найти минимум функции
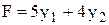
при условиях
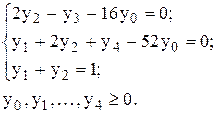
Система ограничений задачи содержит всего одну базисную переменную y4. Поэтому составим расширенную задачу путем введения двух искусственных переменных y5 и у6. :
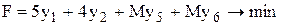
при условиях
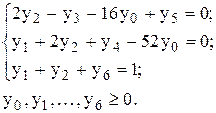
Решение задачи методом искусственного базиса приведено в табл. 10.
Таблица 10
| xd | cd | b | M | M | |||||
| y1 | y2 | y3 | y4 | y0 | y6 | y5 | |||
| Y5 | М | 2 | -1 | -16 | |||||
| y4 | -52 | ||||||||
| y6 | М | ||||||||
| -5 | -4 | ||||||||
| -1 | -16 | ||||||||
| y2 | -1/2 | -8 | |||||||
| y4 | 1 | -36 | |||||||
| y6 | M | 1/2 | -6 | ||||||
| -1 | -2 | -32 | |||||||
| M | 1/2 | -6 | |||||||
| y2 | -1/2 | -8 | |||||||
| y1 | -36 | ||||||||
| y6 | M | -1/2 | -1 | 30 | |||||
| -16/3 | -220 | ||||||||
| M | -1/2 | -1 | |||||||
| y2 | 8/30 | -19/30 | -8/30 | ||||||
| y1 | 36/30 | 12/30 | -6/30 | ||||||
| y0 | 1/30 | -1/60 | -1/30 | ||||||
| 220/30 | -12/30 | -72/30 |
Из таблицы видно, что оптимальным планом задачи является
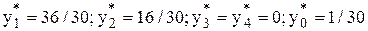 .
.
Учитывая, что 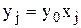 , находим оптимальный план исходной задачи:
, находим оптимальный план исходной задачи:
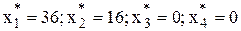 . F(X*)=220/30.
. F(X*)=220/30.
Решение задач линейного программирования транспортного типа
Пусть имеется m пунктов отправления 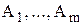 , из которых сосредоточен однородный груз в количестве
, из которых сосредоточен однородный груз в количестве 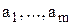 единиц, и n пунктов назначения
единиц, и n пунктов назначения 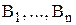 , потребности которых в грузе составляют
, потребности которых в грузе составляют 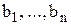 единиц. Стоимость перевозки единицы груза из пункта Ai в пункт Bj равна сij. Необходимо составить такой план перевозки грузов (т.е., определить сколько единиц груза необходимо перевезти из каждого пункта отправления в каждый пункт назначения), который бы обеспечивал вывоз всех грузов из пунктов отправления, удовлетворение всех потребностей в пунктах назначения и имел бы минимальную стоимость.
единиц. Стоимость перевозки единицы груза из пункта Ai в пункт Bj равна сij. Необходимо составить такой план перевозки грузов (т.е., определить сколько единиц груза необходимо перевезти из каждого пункта отправления в каждый пункт назначения), который бы обеспечивал вывоз всех грузов из пунктов отправления, удовлетворение всех потребностей в пунктах назначения и имел бы минимальную стоимость.
Обозначим через xij количество груза, перевозимого из пункта Ai в пункт Bj.
Условия транспортной задачи обычно записывают в виде таблицы, называемой матрицей планирования.
| Пункты отправления | Пункты назначения | Запасы | ||||
| B1 | … | Bj | … | Bn | ||
| A1 | c11 | c1j | c1n | a1 | ||
| x11 | x1j | x1n | ||||
| … | … | |||||
| Ai | ci1 | cij | cin | ai | ||
| xi1 | xij | xin | ||||
| … | … | |||||
| Am | cm1 | cmj | cmn | am | ||
| xm1 | xmj | xmn | ||||
| Потребности | b1 | bj | bn |
Математическая модель данной задачи имеет следующий вид:
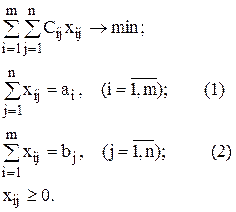
Целевая функция определяет общую стоимость перевозок. Система ограничений (1) обеспечивает вывоз всех грузов из каждого пункта отправления, система ограничений (2) – удовлетворение необходимых потребностей в грузах во всех пунктах назначения.
Всякое неотрицательное решение СЛАУ, задающей систему ограничений (1) – (2), называется планом транспортной задачи. План 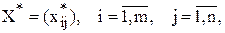 при котором целевая функция минимальна, называется оптимальнымпланом.
при котором целевая функция минимальна, называется оптимальнымпланом.
Теорема
Если запасы грузов a1, …, am и потребности в грузах b1, …, bm – целые числа, то
а) если задача имеет единственное решение, то оно целочисленно;
б) если задача имеет не единственное решение, то среди них имеется хотя бы одно целочисленное.
Модель транспортной задачи называется закрытой, если общая потребность в грузе в пунктах назначения равна общему запасу груза в пунктах отправления, т.е.
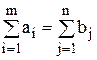 .
.
В противном случае модель ТЗ называется открытой.
Теорема
Для разрешимости транспортной задачи необходимо и достаточно, чтобы ее модель была закрытой.
Приведение открытой модели транспортной задачи к закрытой осуществляется следующим образом:
1) Если запасы больше потребностей: 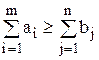 , вводится фиктивный (n+1)-й пункт назначения. Его потребность
, вводится фиктивный (n+1)-й пункт назначения. Его потребность 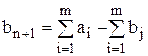 , а тарифы
, а тарифы 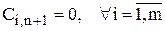 .
.
2) Если 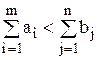 , то вводится фиктивный (m+1)-й пункт отправления, его запас
, то вводится фиктивный (m+1)-й пункт отправления, его запас 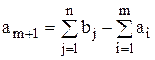 , и тарифы
, и тарифы 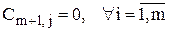 .
.
Особенности транспортной задачи
1. Транспортная задача – это задача линейного программирования, записанная в канонической форме
2. Все коэффициенты ограничений транспортной задачи равны 0 или 1.
3. Всякая переменная 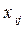 входит только в два уравнения системы ограничений: в i-е уравнение системы (1) и в j-е уравнение системы (2).
входит только в два уравнения системы ограничений: в i-е уравнение системы (1) и в j-е уравнение системы (2).
4. Число переменных xij в задаче равно (mn).
5. Число ограничений в ТЗ равно (m + n).
6. Если сложить почленно все уравнения системы (1) и все уравнения системы (2), то получатся два одинаковых уравнения. Это значит, что уравнения системы ограничений являются линейно зависимыми. Одно из них можно выразить через другие. Ранг матрицы ограничений n+m-1, опорный план ТЗ содержит n+m-1 отличную от нуля компоненту.
Если опорный план ТЗ содержит (n + m – 1) не равный нулю компонент, то опорный план называется невырожденным, если меньше (m + n – 1) - вырожденным.
Определение опорного плана ТЗЛП
Как и в симплекс методе, решение задачи транспортной задачи линейного программирования осуществляется в 2 этапа:
1) Построение первоначального опорного плана ТЗ.
2) Его улучшение.
При построении начального опорного плана на каждом шаге в таблице заполняют одну клетку, которую называют занятой. При заполнении клетки либо полностью обеспечивается потребность в грузе у одного из потребителей (в этом случае столбец, содержащий занятую клетку, исключается из дальнейшего рассмотрения), либо полностью обеспечивается вывоз груза от одного из поставщиков (исключается строка). Всего при построении опорного плана выполняется (m + n – 1) шаг.
Рассмотрим 2 метода определения ОП ТЗ.
Метод северо-западного угла
Заполнение клеток начинается с левой верхней клетки таблицы («северо-западный угол») и заканчивается заполнением клетки 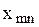 ( правой нижней ).
( правой нижней ).
Пример:
C=180*5+10*4+190*7+10*4+140*6+20*8+100*5=3810
| Пункты отправления | Пункты назначения | ||||
| B1 | B2 | B3 | B4 | ||
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 | |||||
| Потребности |
Замечание: Если на каждом шаге определяется перевозка 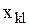 , а при этом
, а при этом 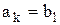 , то
, то 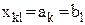 , вычеркивается либо строка k, либо столбец l, а в следующую заполняемую клетку помещается нулевая перевозка, и эта клетка считается занятой. При этом нулевая перевозка помещается в ту из соседних клеток, которой соответствует минимальный тариф.
, вычеркивается либо строка k, либо столбец l, а в следующую заполняемую клетку помещается нулевая перевозка, и эта клетка считается занятой. При этом нулевая перевозка помещается в ту из соседних клеток, которой соответствует минимальный тариф.
Метод северо-западного угла обеспечивает построение опорных планов, которые часто оказываются далекими от оптимальных. Более близкие к оптимальным планы можно получить с помощью метода минимального элемента.
Метод минимального элемента
На каждом шаге выбирается для заполнения клетка, имеющая минимальный тариф. Если таких клеток несколько, то выбирается любая из них.
Рассматриваются пункты отправления и назначения, соответствующие выбранной клетке, и в ней записывается максимально возможная перевозка. Затем из рассмотрения исключают либо строку, соответствующую пункту отправления, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены.
Пример:
C=70*3+120*2+20*4+100*7+80*4+160*3+100*3=2330
| Пункты отправления | Пункты назначения | ||||
| B1 | B2 | B3 | B4 | ||
| A1 | (4 шаг) 3 | (1 шаг) 2 | |||
| A2 | (5 шаг) 4 | (7 шаг) 7 | (6 шаг) 4 | ||
| A3 | (2 шаг) 3 | ||||
| A4 | (3 шаг) 3 | ||||
| Потребности |
Метод потенциалов получения опорного плана транспортной задачи
Рассмотрим транспортную задачу и запишем к ней двойственную. Для этого каждому ограничению прямой задачи поставим в соответствие двойственную переменную. При этом двойственные переменные, соответствующие ограничениям (1), обозначим через ui, а соответствующие (2) - vj. Тогда
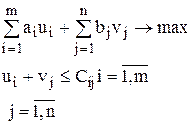
Числа ui и vj называют потенциалами соответственно пунктов отправления и назначения. Для того, чтобы план исходной задачи был оптимален, необходимо:
1). 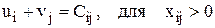 (т. е. для занятых клеток таблицы сумма потенциалов равна тарифу, записанному в этой клетке).
(т. е. для занятых клеток таблицы сумма потенциалов равна тарифу, записанному в этой клетке).
2). 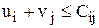 ,
, 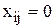 , т.е. для свободной клетки сумма потенциалов меньше или равна тарифу.
, т.е. для свободной клетки сумма потенциалов меньше или равна тарифу.
Если хоть одна свободная клетка не удовлетворяет условию (2), то план является неоптимальным, и его можно улучшить, вводя в базис клетку, для которой нарушено условие оптимальности.
Алгоритм метода потенциалов:
1). Построение первичного опорного плана.
2). Определение потенциалов пунктов отправления (ui) и пунктов назначения (vj).
Потенциалы находят из системы уравнений ui + vj = Cij, где Cij - тарифы, стоящие в заполняемых клетках таблицы. Число переменных в этой системе равно m + n, число уравнений (m + n – 1). Для нахождения решения системы один из потенциалов приравнивается произвольному числу (например, u1=0) и последовательно находятся значения всех остальных потенциалов.
3). Проверка оптимальности плана.
Проверяем условия (2): 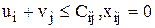 . Вычисляем
. Вычисляем 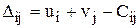 - оценки свободных переменных для оптимального базиса. Если все
- оценки свободных переменных для оптимального базиса. Если все 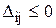 , то получаемый план является оптимальным, иначе - к шагу 4.
, то получаемый план является оптимальным, иначе - к шагу 4.
4). Выбор переменной для включения в базис (выбор клетки, в которую необходимо послать переменную).
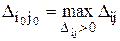 . Если таких клеток несколько, то для заполнения выбирается клетка, имеющая минимальный тариф.
. Если таких клеток несколько, то для заполнения выбирается клетка, имеющая минимальный тариф.
5). Построение цикла пересчета для выбранной свободной клетки i0 j0.
Циклом в таблице условий ТЗ называется ломаная линия, которая начинается в свободной клетке, и вершины которой (кроме начальной) расположены в занятых клетках, а звенья параллельны строкам и столбцам. При правильном построении опорного плана для каждой свободной клетки таблицы можно построить только один цикл.
После построения цикла его вершины последовательно отмечаются знаками “+” и “-”, причем свободной клетке приписывается знак “+”.
6). Определение величины перераспределения груза.
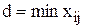 , где xij - перевозки, стоящие в вершинах цикла, отмеченных знаком “-”. Клетку, которой соответствует d, обозначим через i1 j1.
, где xij - перевозки, стоящие в вершинах цикла, отмеченных знаком “-”. Клетку, которой соответствует d, обозначим через i1 j1.
7). Сдвиг по циклу пересчета (перераспределение грузов).
В выбранную для заполнения свободную клетку (i0,j0) заносится значение d. Одновременно это число прибавляется к значениям перевозок, стоящих в клетках со знаком “+”, и вычитается из значений перевозок, стоящих в клетках со знаком “–”. Т.о. клетка (i0, j0) становится занятой, а i1 j1 - свободной.
Замечание: при сдвиге по циклу пересчета число занятых клеток остается const = n + m – 1. Если d соответствует нескольким клеткам таблицы, то освобождают одну из них, а в остальные записываются нулевые перевозки и считают их занятыми. Нулевые перевозки записываются и в клетки, которые имеют меньшие тарифы.
8). Переход к шагу 2.
Замечание: если при построении двойственной задачи, одну двойственную переменную обозначают через ui, а другую через vj, то условие оптимальности:
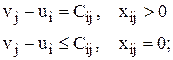
Пример:
| B1 | B2 | B3 | B4 | ||
    A1 A1
| + 4 | – 3 | |||
| A2 | – 7 | + 4 | |||
| A3 | |||||
| A4 | |||||
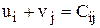 - занят.
- занят.
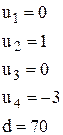
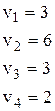
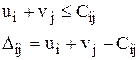
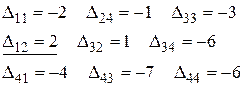
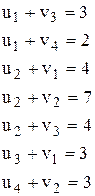
| B1 | B2 | B3 | B4 | ||
   A1 A1
| + 4 | – 2 | |||
 A2 A2
| – 7 | + 4 | |||
| A3 | |||||
| A4 | |||||
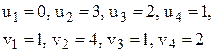
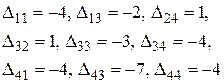
| B1 | B2 | B3 | B4 | ||
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 | |||||
Пересчитав u, v и D, получим, что это оптимальный план ( 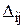 <0).
<0).
Общая стоимость перевозок равна 2160.
Прикладные задачи транспортного типа.
В формальных терминах ТЗ формулируется большое количество задач, не связанных с перевозками продуктов. Это задачи, связанные с планированием информационных потоков, размещением заказов и загрузкой оборудования, заключением контрактов, назначением персонала, распределением ресурсов и т.д. Все эти задачи называются задачами транспортного типа.
1. Задача выбора (задача о назначениях)
Имеется n исполнителей и n видов работ, которые они могут выполнять. 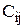 - производительность i-го исполнителя при выполнении j работы. Каждый исполнитель может выполнять один вид работ, каждая работа может быть выполнена одним исполнителем. Требуется таким образом распределить исполнителей по видам работ, чтобы общая производительность была максимальной.
- производительность i-го исполнителя при выполнении j работы. Каждый исполнитель может выполнять один вид работ, каждая работа может быть выполнена одним исполнителем. Требуется таким образом распределить исполнителей по видам работ, чтобы общая производительность была максимальной.
Введем переменные 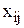 , где
, где 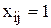 , если i-й исполнитель назначен на j-работу,
, если i-й исполнитель назначен на j-работу, 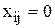 - иначе.
- иначе.
Модель:
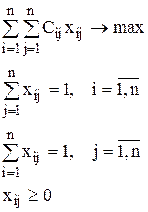
Иногда задача о назначениях формулируется как целочисленная (т.е. добавляется условие xij = 1 или xij = 0). Однако это требование излишне, т.к. если аiи biцелочислены "i, j, то opt план ТЗ тоже будет целочисленным.
Иногда задача о назначениях формулируется как задача минимизации, если в качестве 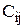 используется время, затраченное i-тым исполнителем на выполнении j-той работы.
используется время, затраченное i-тым исполнителем на выполнении j-той работы.
Если рассматривается задача максимизации, то, умножив целевую функцию на (–1), переходим к обычной ТЗ.
Иногда используется следующий метод: в каждой строке находится максимальная производительность и приравнивается к 0.
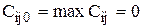 .
.
Остальные производительности считаются следующим образом:
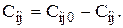
Примеры задач о назначениях:
Ø закрепление исполнителей за видами работ;
Ø закрепление за станками операций по обработке деталей;
Ø назначение претендентов на вакантные места при составлении штатного расписания.
Задачу о назначениях можно обобщить, если имеются идентичные работы и лица, которые могут их выполнить с одинаковой производительностью. Тогда рабочих можно объединить в группы, а работы – в категории.
Пусть имеется m групп лиц Ai (i = 1,…, m) по ai человек в каждой и n категорий работ Bj (j = 1,…, n) по bj единиц в каждой. Известна производительность Cij лица i-той группы при выполнении j-той категории работ. Необходимо определить, сколько лиц из каждой группы и на какую категорию работ назначить, чтобы суммарная производительность была максимальной.
Обозначим через xij количество лиц i-той группы, назначенных для выполнения работ j-той категории. Тогда задача имеет следующую математическую модель:
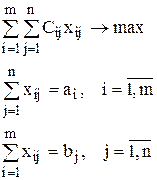
Предполагается, что 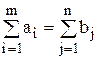 .
.
Если 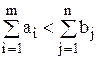 , вводят фиктивную группу лиц, если наоборот – фиктивную категорию работ.
, вводят фиктивную группу лиц, если наоборот – фиктивную категорию работ.
Пример. Задача планирования, подготовки и распределения кадров.
Пусть b1 … bn – вакантные должности, а1 … аm – категории специалистов различных профилей, подлежащих распределению.
Пригодность специалиста i-того профиля при назначении его на должность j обозначим числом Cij. Тогда модель – см. выше.
xij – количество выпускников специальности i, планируемое на замещение должности j.
Задача о назначениях может быть решена методом потенциалов. Но она имеет особенности. В каждом столбце ТЗ стоит по одной единице, причем они располагаются в различных строках. Опорный план такой задачи является вырожденным, т.к. содержит n отличных от нуля компонент.
2. Распределительная задача
В моделях ТЗ речь шла о перевозке однородного продукта. Естественно, что на практике чаще возникает задача перевозки ряда продуктов. Если рассматриваемые продукты качественно совершенно различны (например, уголь, цемент, сахар), то задача определения opt плана перевозок распадается на ряд обычных ТЗ (по углю, цементу, сахару).
Однако во многих случаях продукты, подлежащие перевозке, частично взаимозаменяемы. Тогда возникает необходимость в решении ТЗ для неоднородного продукта.
Задачи оптимального распределения взаимозаменяемых ресурсов получили название распределительных задач.
Постановка задачи. Найти оптимальное распределение m различных взаимозаменяемых ресурсов, имеющихся в количествах а1 … аm для удовлетворения n различных потребностей b1 … bn при заданных значениях Cij – оценки использования i-того ресурса на удовлетворение j-х потребностей; li – количество единиц j-х потребностей, которые удовлетворяются единицей i-х ресурсов.
Тогда модель:
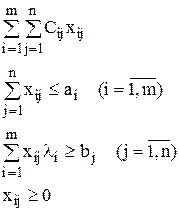
Здесь xij – количество единиц i-х ресурсов, используемых для удовлетворения j-х потребностей.
Если через xij обозначить количество единиц j-х потребностей, которые обеспечиваются ресурсами i-того вида, то получится эквивалентная модель:
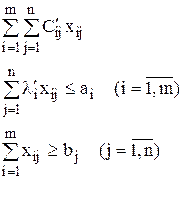
где 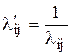 – количество единиц i-того ресурса, необходимого для удовлетворения единицы j-х потребностей. Cij – оценки единицы j-х потребностей, которые обеспечиваются i-ми ресурсами.
– количество единиц i-того ресурса, необходимого для удовлетворения единицы j-х потребностей. Cij – оценки единицы j-х потребностей, которые обеспечиваются i-ми ресурсами.
Дата добавления: 2016-06-02; просмотров: 2537;
