ІІІ.9. Властивості поверхневих потенціалів. Поверхні Ляпунова.
Відповідно до того, як були введені потенціали для випадку поверхневого потенціалу простого шару, маємо формулу 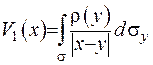 . У двовимірному випадку він зображується за формулою
. У двовимірному випадку він зображується за формулою 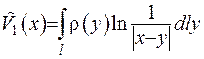 . Потенціали подвійного шару зображуються наступним чином:
. Потенціали подвійного шару зображуються наступним чином: 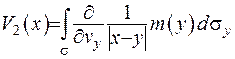 - у трьохвимірному випадку, та
- у трьохвимірному випадку, та 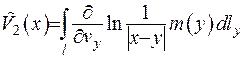 - у двовимірному.
- у двовимірному.
Як було доведено раніше, якщо точка  не належить поверхні
не належить поверхні 
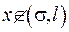 та
та 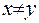 , то усі потенціали є гармонічними функціями.
, то усі потенціали є гармонічними функціями.
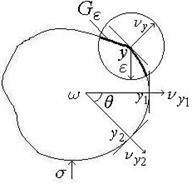
Проілюструємо на рисунках основні позначення: внутришню область, де функція є гармонічною, позначимо як 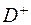 , зовнішню як
, зовнішню як 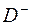 ,
, 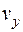 - нормаль.
- нормаль.
Для двовимірного випадка – див.рис.2.
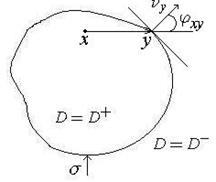
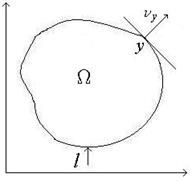
Якщо точка  належить поверхні
належить поверхні  , то гармонічність може бути нарушено, бо підінтегральна функція може перетворюватися на нескінченність, тобто буде отримано невласний інтеграл. На питання умов його існування дав відповідь видатний російський вчений О.Г.Ляпунов. Їм було введено для цього нове поняття – поверхні Ляпунова.
, то гармонічність може бути нарушено, бо підінтегральна функція може перетворюватися на нескінченність, тобто буде отримано невласний інтеграл. На питання умов його існування дав відповідь видатний російський вчений О.Г.Ляпунов. Їм було введено для цього нове поняття – поверхні Ляпунова.
Поверхню називають поверхнею Ляпунова, якщо виконано три умови:
1) У кожній точці поверхні існує дотична площина;
2) Якщо у будь-який точці дотику побудувати кулю достатньо малого радіусу, то ця куля ділитиме всю поверхню, на дві – поверхню, що лежить усередині сфери та зовні: 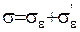 . Або іншими словами: якщо з будь-якої точки кулі провести лінію паралельну до нормалі, то вона перетинатиме поверхню тільки один раз (що дозволяє ввести локальну систему координат
. Або іншими словами: якщо з будь-якої точки кулі провести лінію паралельну до нормалі, то вона перетинатиме поверхню тільки один раз (що дозволяє ввести локальну систему координат 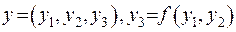 .
.
3) Якщо взяти дві точки 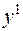 та
та 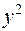 на поверхні та провести нормалі до них
на поверхні та провести нормалі до них 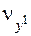 та
та 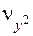 , то
, то 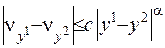 , де
, де 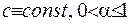 , або
, або 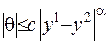 .
.
 Таким чином, якщо поверхня
Таким чином, якщо поверхня  є поверхнею Ляпунова, то невласній іетеграл буде існувати.
є поверхнею Ляпунова, то невласній іетеграл буде існувати.
Дата добавления: 2016-05-05; просмотров: 676;
