ІІІ.11. Розривні властивості потенціалу подвійного шару.
 Нехай точки
Нехай точки 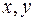 належать поверхні
належать поверхні  . Виберемо точку
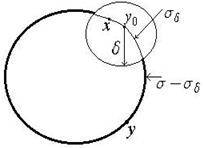
. Виберемо точку 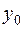 , що також лежить на цієї поверхні, та побудуємо коло з центром в точці
, що також лежить на цієї поверхні, та побудуємо коло з центром в точці 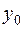 радіуса
радіуса  (див.рис. ). Його поверхню позначимо
(див.рис. ). Його поверхню позначимо
Введемо допоміжну функцію  (ІІІ.17)
(ІІІ.17)
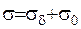 , де
, де  ,
,  - поверхня Ляпунова.
- поверхня Ляпунова.
Покажемо, що, якщо 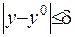 , де
, де 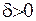 - будь-яка мала величина, то має місце оцінка
- будь-яка мала величина, то має місце оцінка
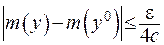 , (ІІІ.43)
, (ІІІ.43)
де 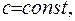
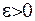 - як завгодно мале число.
- як завгодно мале число.
Для доведення цього факту виведемо певні попередні оцінки.
Нехай 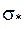 - деяка частина поверхні
- деяка частина поверхні  . Доведемо оцінку інтеграла
. Доведемо оцінку інтеграла 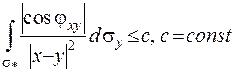 . Розглянемо для цього дві функції
. Розглянемо для цього дві функції
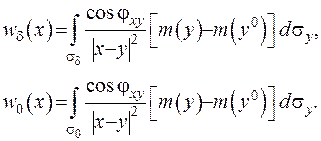 (ІІІ.44)
(ІІІ.44)
Побудуємо їх різницю та покажемо, що вона може бути як завгодно малою:
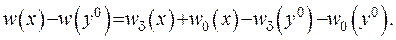 (ІІІ.45)
(ІІІ.45)
Тут  - довільна точка, що може лежати як усередині, так і зовні. Продовжимо міркування у правій частині рівності (ІІІ.45):
- довільна точка, що може лежати як усередині, так і зовні. Продовжимо міркування у правій частині рівності (ІІІ.45):
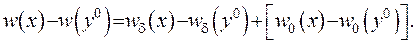 (ІІІ.46)
(ІІІ.46)
Виходимо з відомої нерівності, що 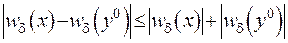 . Враховуючи це, запишемо:
. Враховуючи це, запишемо:
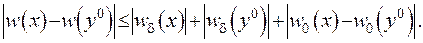 (ІІІ.47)
(ІІІ.47)
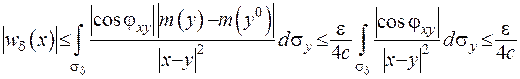 (ІІІ.48)
(ІІІ.48)
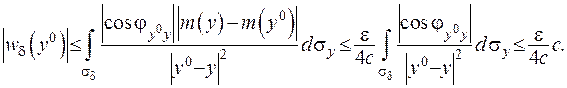
Далі отримаємо оцінку останнього доданку у нерівності (ІІІ.47):
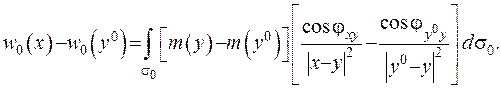 (ІІІ.49)
(ІІІ.49)
або
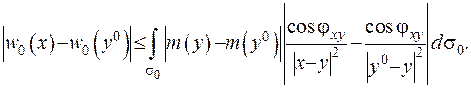
Якщо припустимо, що у всійї області  густини обмежені, то з цього випливає, що
густини обмежені, то з цього випливає, що 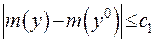 . А якщо
. А якщо 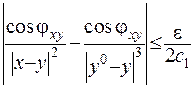 , то остаточно отримаємо з урахуванням нерівності (ІІІ.49) :
, то остаточно отримаємо з урахуванням нерівності (ІІІ.49) :
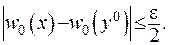 (ІІІ.50)
(ІІІ.50)
Отже, враховуючи отримані оцінки (ІІІ.48) та (ІІІ.50), завершимо оцінку (ІІІ.47):
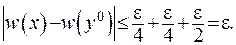 (ІІІ.51)
(ІІІ.51)
Ми показали, що допоміжно введена функція 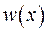 за формулою (ІІІ.42) є неперервною, і можна записати її у формі:
за формулою (ІІІ.42) є неперервною, і можна записати її у формі:
 (ІІІ.52)
(ІІІ.52)
або
 (ІІІ.53)
(ІІІ.53)
Розглянемо три випадки розташування точки  :
:
1) Якщо 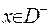 , то
, то 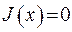 , звідки маємо
, звідки маємо 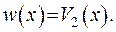
2) Якщо 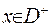 , то
, то 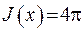 , звідки маємо
, звідки маємо 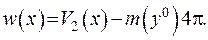 .
.
3) Якщо 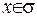 -
- 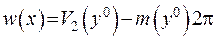 ,
,
У випадку, коли  належить поверхні, можемо взяти
належить поверхні, можемо взяти  . Матимемо значення потенціалу
. Матимемо значення потенціалу 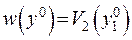 , яке називають прямим значенням потенціалу.
, яке називають прямим значенням потенціалу.
Розглянемо предельні значення. З формули 2) випливає, що, якщо 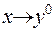 (тобто підходом до неї з боку
(тобто підходом до неї з боку 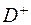 ) (так як
) (так як 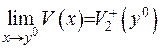 ), то можна записати
), то можна записати 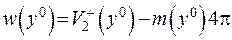 . З іншого боку, з 1) випливає, що
. З іншого боку, з 1) випливає, що 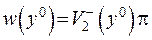 , якщо підходимо до точки з боку області
, якщо підходимо до точки з боку області 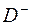 . Отже. маємо
. Отже. маємо
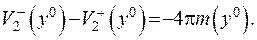 (ІІІ.54)
(ІІІ.54)
Співвідношення (ІІІ.54) визначає стрибок потенціалу подвійного шару під час переходу через поверхню.
Дата добавления: 2016-05-05; просмотров: 720;
