ІІІ.12. Зведення задачі Діріхлє до інтегрального рівняння. Доведення існування його розв’язку.

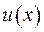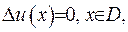Для задачі Діріхлє, де потрібно відшукати гармонічну функцію в області , тобто якщо на границі області гармонічності задано значення функції , раніше було доведено єдність розв’язку та його стійкість. Щоби завершити доведення коректності задачі Діріхлє, потрібно доказати її розв’язуємость.

Нехай 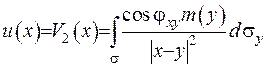. Якщо точка не належить поверхні, то функція 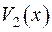є гармонічною функцією:

.

Задовольнимо умові на границі, для чого спрямуємо до 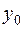, тоді використаємо доведену властивість 2) та з одного боку отримаємо

,

з іншого боку з властивості 3) випливає

.

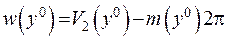Приравнявши ліві частини рівностей, маємо

,

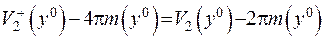або

.

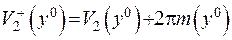Остаточно отримано:

.

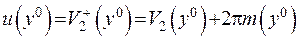З іншого боку, 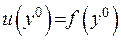. Дорівнявши обидві частини цих рівностей , маємо:

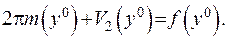(ІІІ.55)

Поділимо обидві частини співвідношення (ІІІ.55) на та запишемо зображення потенціалу подвійного шару:

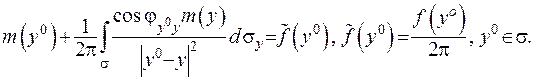(ІІІ.56)

Отримали інтегральне рівняння (ІІІ.56) відносно невідомої функції густини потенціалу 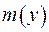. Доведемо його розв’язуємость.

З цією метою спершу розглянемо наступне інтегральне рівняння Фредгольма

(ІІІ.57)

Якщо у рівнянні (ІІІ.57) взяти 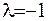, а 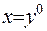, то отримаємо вихідне інтегральне рівняння (ІІІ.56). Відповідно до відомої альтернативи Фредгольма, для єдинності та розв’язуємості інтегрального рівняння (ІІІ.57)

з неперервним ядром (або ядром з особливістю типу полюсу) при неперервній правій частині, необхідно та достатньо, щоб однорідне рівняння (ІІІ.57)

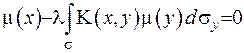(ІІІ.58)

мало тільки тривіальний розв’язок. Ті значення 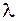, при яких існує ненульовий розв’язок, називають власними числами інтегрального рівняння.

У відповідності з вищезазначеним, мусимо довести, що однорідне рівняння

(ІІІ.59)

має тільки тривіальний розв’язок. Це можна зробити, якщо довести, що 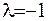не є власним числом для рівняння:

(ІІІ.60)

Припустимо, що поверхня є поверхнею Ляпунова, причому опуклою. Тоді 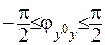. З останнього випливає, що 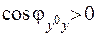. Це є справедливим тільки для опуклої поверхні. Будемо вважати, що 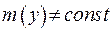та є неперервною функцією на поверхні . Отже, відшукується така точка 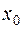, в який функція 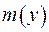сягає свого максимуму. З рівності (ІІІ.60) маємо:

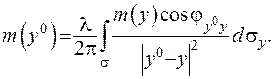(ІІІ.61)

Зробимо наступну оцінку:

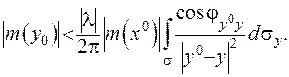(ІІІ.62)

Останній множник у правій частині нерівності (ІІІ.62) є інтегралом Гауса на поверхні. Раніше було доведено, що його значення дорівнює . З цього випливає, що

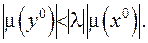(ІІІ.63)

Щоб така строга нерівність виконувалася, необхідно, щоби 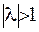, а з цього маємо, що 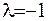не може бути власним числом. Отже, рівняння (ІІІ.60) має тільки тривіальний розв’язок, а вихідне рівняння у такому випадку має єдиний розв’язок, який завжди існує.

Розглянемо випадок, коли . Відповідне однорідне рівняння (ІІІ.60) прийме вигляд:

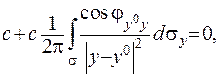
або Звідки отримаємо, що дорівнюватиме нулеві.