ІІІ.2. Об’ємні та поверхневі потенціали.

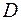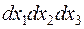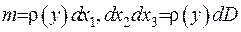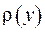З’ясуємо, який потенціал буде утворюватися масою, що розподілена у деякому об’ємі .Для цього розіб’ємо об’єм на нескінченно малі паралелепіпеди. Виберемо серед них елементарний паралелепіпед довільного об’єма та знайдемо його елементарну масу , де - густина. Припускаючи, що тіло є однорідним, підсумовуваємо потенціали кожного елементу 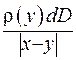. Підсумовування нескінченно малих приведе до інтеграла

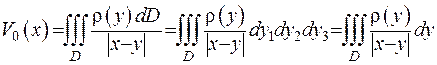(ІІІ.4)

Формула (ІІІ.4) описує об’ємний (Ньютоновський) потенціал. Якщо 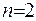, то, використовуючи описану вище технологію, отримаємо

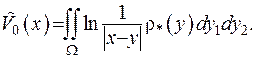(ІІІ.5)

Це і є логарифмічний потенціал маси, що розподілений на площині 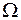з густиною .

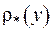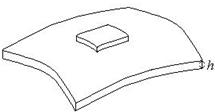Розглянемо масу, що розподілена на поверхні 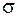(див. рис.), де розташована оболонка товщини .

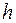Виділимо нескінченно малий елемент оболонки, його об’єм дорівнюватиме 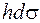, а маса у точці 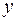на серединній поверхні визначатиметься виразом 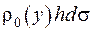або, якщо ввести функцію 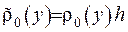, то маса дорівнюватиме 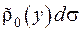. Тоді потенціал простого шару запишемо за формулою

.

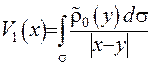Якщо 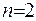, замість поверхні розглянемо вісь стрижня довжини 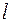. Вибираючи його елементарну ділянку 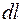та припускаючи, що густину, що віднесена до одиниці довжини стрижня 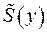, запишемо логаріфмичний потенціал простого шару

.

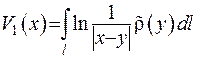ІІІ.2.Діполі та потенціал подвійного шару.

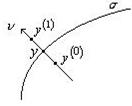Під час викладення наступного матеріалу буде застосовано поняття “від’ємна маса”, що з фізичної точки зору є неможливим. Для того, щоб внести фізичну трактовку цього поняття, легше уявити від’ємно та додатньо заряджені маси, що, як відомо, має місце у елесктростатиці.

Розглянемо поверхню 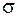та виберемо на ній точку 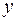. Проведемо нормаль 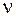в цієй точці та візьмемо на нормалі точки 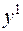та 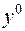. Будемо вважати, що у точці 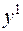зосереджена додатня маса, а у точці 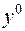- від’ємна. Відшукаємо потенціал силового поля, що утворюється ціми масами:

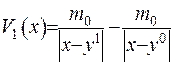. (ІІІ.6)

Формула (ІІІ.6) нагадує формулу з механіці, де визначено пару сил. Діполем будемо називати дві маси, що однакові за величиною та протилежно заряджені. Визначимо момент діполя за формулою 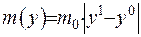. Знайдемо межу потенціалу силового поля, прямуючи 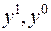до точки 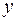(враховуючи при цьому, що 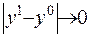, коли ):

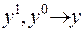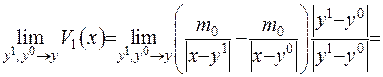
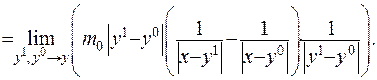
Множник 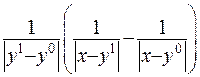- це є прирощення фундаментальної функції 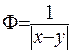, а множник 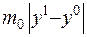- момент діполя. Отже, отриман 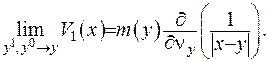(ІІІ.7)

Формула (ІІІ.7) визначає силове поле діполя.

Маємо зазначити, що аналогічні міркування проводяться у механіці під час виведення величини зосередженого моменту у заданій точці. Процедура виведення складається з того, що зближають сили, які утворюють пару сил, збільшуя їх величину так, щоб момент пари залишався незмінним та рівним зосередженому моменту. Аналогічним чином, під час виведення формули (ІІІ.7), зближуючи відстань, водночас збільшуємо масу так, щоб момент діполя залишався незмінним.

Введемо до розгляду потенціал подвійного шару. З цією метою уявимо два шару, срединни поверхні яких паралельні одна до одної та паралельні поверхні 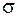. Припустимо, що один з шарів заряджен додатньо, а інший – від’ємно.

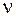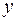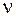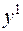Проведемо нормаль до поверхні у точці . В кожному з шарів виберемо на нормалі точки та 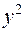симетрично відносно точки 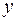таким чином, щоб напрямок від 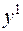до 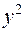збігався з напрямком вектора 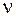. У точках 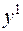та 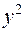кожного з шарів розташуємо маси, що заряджені протилежними за знаком зарядами. Це утворює різницю потенціалів

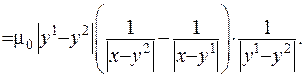
Спрямуєм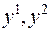о до 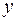так, щоб величина момента діполя 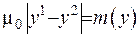залишалася постійною. Тоді потенціал діполя у точці 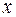буде наступним:

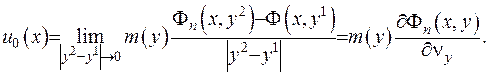(ІІІ.8)

Отже, силове поле нескінченно малого участка дорівнюватиме 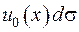. Знайдемо потенціал у точці 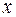, що утворюється всіма діполями, які розподілені на поверхні :

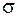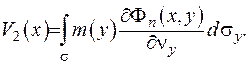(ІІІ.9)

Якщо 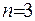, то інтеграл (ІІІ.9) називають потенціалом подвійного шару. Якщо 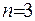то логарифмічним потенціалом подвійного шару:

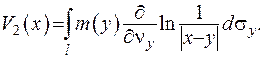(ІІІ.10)