Показатели анализа рядов динамики
Для характеристики интенсивности изменения во времени в статистике используются следующие показатели:
— абсолютный прирост;
— темпы роста;
— темпы прироста;
— абсолютное значение 1% прироста.
Перечисленные показатели могут характеризовать динамику явления по отношению к предыдущему периоду либо за интервал, включающий в себя несколько периодов. В соответствии с целью исследования различают цепные и базисные показатели динамики.
В том случае, если сравнение производится с периодом или моментом времени, начальным в ряду динамики, то имеют в виду базисный показатель динамики.
В том же случае, если сравнение производится с предыдущим годом или моментом, тогда говорят о цепных показателях динамики.Расчет показателей динамики приведен в табл. 1.
Таблица 1
Расчет показателей динамики
| Показатель | Базисный | Цепной | Взаимосвязь между ними |
| 1. Абсолютный прирост, ∆ | y1 – y0 | yi – yi-1 | ∆баз= 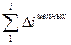
|
| 2. Темп роста, Тр | y1 / y0 (100%) | yi / yi-1(100%) | 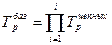
|
| 3. Темп прироста, Тпр | Тр-1
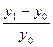
| Тр-1
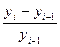
| - |
| 4. Абсолютное значение 1 % прироста, А(%) | - | 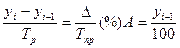
| - |
Существует взаимосвязь между цепными и базисными абсолютными приростами и темпами роста (3 графа, таблица 1). Если сложить все цепные абсолютные приросты, получим абсолютный базисный прирост за весь период (за который были рассчитаны цепные приросты). Если найти произведение цепных темпов роста, получим базисный темп роста.
Помимо оценки интенсивности динамических процессов необходимо дополнить показатели динамики расчетом их средних,а именно:
— средний уровень ряда;
— средний абсолютный прирост;
— средний темп роста;
— средний темп прироста.
1. Методика расчета среднего уровняопределяется видом ряда динамики.
Если ряд динамики интервальный, то считают по средней арифметической простой.
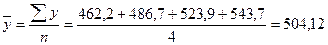
Для моментного ряда применяют среднюю хронологическую:
§ простую, если моменты времени равно отстают (через год, месяц):
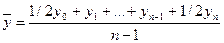
где п — число дат;
(п -1) — число периодов.
- взвешенную, если интервалы между датами различны, тогда формула выглядит следующим образом:
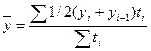
ti - продолжительность интервала от i-ой даты до i + 1.
Пример расчета средней хронологической взвешенной.
Имеются данные о численности трудовых ресурсов области за ряд лет (табл. ниже).
| Показатель | 01.01.89 | 01.01.93 | 01.01.94 | 01.01.99 |
| Трудовые ресурсы, млн.чел. | 1,8 | 2,1 | 2,5 | 3,0 |
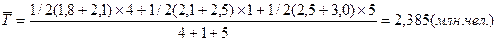
где 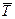 - средняя годовая численность трудовых ресурсов.
- средняя годовая численность трудовых ресурсов.
Иногда рассчитывают по средней арифметической взвешенной, как:
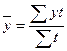
где 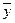 - продолжительность интервала от одной даты до другой:
- продолжительность интервала от одной даты до другой:
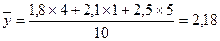
Расчет по средней арифметической является приближенным, так как используется не вся информация.
2. Средний абсолютный приростможет быть рассчитан на основе как цепных, так и базисных абсолютных приростов:
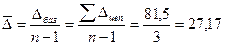
где п – число лет или дат.
3. Средний темп ростатакже рассчитывается на основе либо базисного, либо цепных темпов роста:
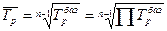
4. Средний темп прироста:
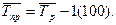
Пример расчета показателей динамики.
На основании имеющихся данных (табл. 3) рассчитать показатели, характеризующие динамику объема произведенной продукции. Сделайте выводы. Результаты расчетов показателей динамики оформим в таблице 4.
Таблица 3
Выпуск продукции за период 1995 – 1998 гг. (млн. руб.)
| Показатель | |||||||
| Производство продукции | 520,2 | 480,7 | 523,9 | 536,7 | 548,3 | 560,0 | 575,2 |
Таблица 4
Динамика выпуска продукции
| Годы | Производство продукции, млн.руб. | Абсолют. прирост, млн. руб. | Темп роста, % | Темп прироста, % | А(%), млн. руб. | |||
| Базисный | Цепной | Базисный | Цепной | Базисный | Цепной | |||
| 520,2 | - | - | 100,0 | - | - | - | - | |
| 480,7 | -39,5 | -39,5 | 92,4 | 92,4 | -7,6 | -7,6 | 52,0 | |
| 523,9 | 3,7 | 43,2 | 100,7 | 109,0 | 0,7 | 9,0 | 48,1 | |
| 536,7 | 16,5 | 12,8 | 103,2 | 102.4 | 3,2 | 2,4 | 52,4 | |
| 548,3 | 28,1 | 11,6 | 105,4 | 102,2 | 5,4 | 2,2 | 53,7 | |
| 560,0 | 39,8 | 11,7 | 107,7 | 102,1 | 7,7 | 2,1 | 54,8 | |
| 575,2 | 55,0 | 15,2 | 110,6 | 102,7 | 10,6 | 2,7 | 56,0 |
Для расчета среднего уровня ряда необходимо определить вид ряда динамики. Так как объем продукцииприводится за год, то есть за интервал времени, следовательно, ряд динамики - интервальный с равными интервалами. Средний уровень ряда рассчитывается по формуле средней арифметической простой.
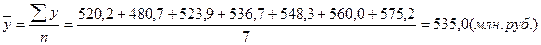
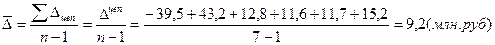
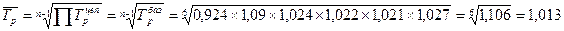
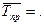 1,013-1 = 0,013 (1,3%)
1,013-1 = 0,013 (1,3%)
На основании рассчитанных показателей динамики можно сделать следующие выводы: объем производства за 7 лет увеличился на 55 млн. рублей, или на 10,6%. В период с 1994 по 1994 г. наблюдался спад производства на 7,6% (39,5 млн. руб.). Затем в последующие годы объем производства постоянно увеличивался. Наибольший рост выпуска произошел в период с 1994 по 1995 г. - на 9%, или на 43,2 млн. руб. В среднем за период объем производства составил 535 млн. руб., выпуск продукции ежегодно увеличивается на 9,2 млн. рублей, или на 1,3%. Общая тенденция - к увеличению роста продукции.
Дата добавления: 2016-12-16; просмотров: 1024;
