Агрегатная форма индексов
Чаще всего используют индексы, представляющие собой сравнение сумм агрегатов.
Используя агрегатную форму индексов,можно охарактеризовать изменение явления в пространстве (территориальные) и во времени. Использование агрегатной формы индексов позволяет сравнивать изменения состояния неоднородных совокупностей. Например, общий индекс цен может быть рассчитан двумя способами:
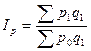 - так называемый индекс Пааше.
- так называемый индекс Пааше.
В приведенном индексе цена на каждый товар взвешена соответствующим объемом продаж. Таким образом, в числителе будет товарооборот отчетного периода, а в знаменателе - товарооборот отчетного периода в базисных ценах. Следовательно, индекс показывает изменение цен при неизменном количестве.
Индекс Пааше наиболее часто используется в экономических расчетах, однако, может быть использован и другой индекс:
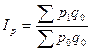 - так называемый индекс Лайспереса.
- так называемый индекс Лайспереса.
Если цену оставить неизменной, а количество проиндексировать (изменить), то получим индекс физического объема:
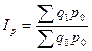 , который будет отражать изменение количества продаж. Здесь цена будет использоваться в качестве соизмерителя.
, который будет отражать изменение количества продаж. Здесь цена будет использоваться в качестве соизмерителя.
Для того чтобы определить общее изменение товарооборота по группе товаров, нужно общий товарооборот в отчетном периоде разделить на общий товарооборот в базисном периоде:
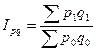
Данный индекс показывает, что на товарооборот влияют два фактора: цена и количество проданного товара, следовательно, индекс может быть представлен в виде двухфакторной мультипликативной модели итогового показателя:
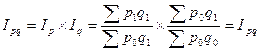
Если взаимосвязь между величинами выражена в форме произведения, либо частного, то эта взаимосвязь сохраняется и для индивидуальных величин.
Правило построения индексовможно сформулировать следующим образом:
В том случае, если индексируется качественный показатель (цена, себестоимость, урожайность, трудоемкость, производительность и т.д.), то веса берутся обычно на уровне отчетного периода. В том же случае, если индексируется количественный показатель (объем производства, количество проданных товаров, численность занятых), то соизмеритель берется на уровне базисного периода.
Перечисленные индексы представлены в виде отношения, поэтому они характеризуют относительное изменение цен, физического объема и товарооборота. Эти же самые индексы могут бытьпредставлены в виде разностей. В этом случае они показывают абсолютное изменение показателя всего и в том числе - за счет отдельных факторов (разложение общего прироста).
Абсолютное изменение общего товарооборота: 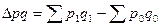 ,
,
в том числе:
- за счет изменения цен: 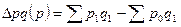 ,
,
- за счет изменения физического объема продаж: 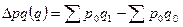 .
.
То же самое можно записать следующим образом:
- за счет изменения физического объема продаж: 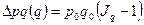 ;
;
- за счет изменения цен: 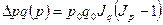 .
.
Агрегатные индексы можно использовать не только при оценке динамики товарооборота, но и общих затрат на производство продукции, валового сбора и т.д.
Пример расчета индивидуальных и агрегатных индексов.
Имеются данные об объеме продаж и ценах на продукты (табл. 1).
Таблица 1
| Товары | Ед. изм. | Базисный период | Отчетный период | Индивид, индексы | |||
| цена, руб. | кол-во | цена, руб. | кол-во | цен | физического объема | ||
| Яблоки | кг | 17.5 | 1,029 | 1,17 | |||
| Яйца | десяток | 14,0 | 1,27 | 0,88 | |||
| Молоко | литр | 6,5 | 7,2 | 1,11 | 0,96 | ||
| Хлеб | булка | 4,5 | 5,0 | 1,11 | 1,18 |
Рассчитайте индивидуальные индексы цен и физического объема по каждому виду товаров. Определите общее изменение товарооборота, цен и физического объема реализации. Рассчитайте сумму переплаты (экономии) покупателей за счет изменения цен.
Индивидуальные индексы цен и физического объема рассчитываются как отношение цены (физического объема) на каждый товар в отчетном периоде к цене (физическому объему) на этот товар в базисном периоде. Результаты расчетов заносятся в таблицу (табл. 1, графы 6, 7).
Для того, чтобы определить относительное изменение товарооборота, рассчитаем общий индекс товарооборота:
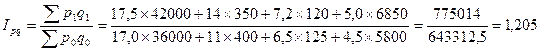
Общий товарооборот увеличился на 20,5%. Рассчитаем индекс цен:
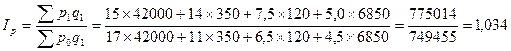
В среднем количество проданных продуктов увеличилось на 16,5%.
Индекс физического объема можно также найти, используя взаимосвязь между индексами:
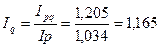 .
.
Для того чтобы найти сумму переплаты или экономии покупателей от изменения цен, необходимо найти разницу между числителем и знаменателем индекса цен:
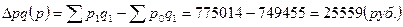
За счет роста цен покупатели заплатили в отчетном периоде за один и тот же объем продуктов на 25559 руб. больше.
Рассмотренные выше индексы используются тогда, когда показатель, изменение которого мы рассматриваем, может быть полечен произведением двух других и изменения этих двух показателей известны. Но в практике расчетов бывает, что абсолютны, значения этих показателей могут быть неизвестны, а известно лишь их относительное изменение и итоговый показатель. В этом случае агрегатные индексы преобразуют в средний арифметический и средний гармонический индекс, в зависимости от того, какими данными мы располагаем.
Пример расчета среднего гармонического индекса.
В розничной торговле ведется учет изменения цен на конкретные товары и учет стоимости проданных товаров (табл. 2). Объем продаж в натуральном объеме не известен. Как определить е этом случае индекс цен?
Таблица 2
| Наименование продукции | Реализация продукции в базисном периоде, тыс. руб. | Реализация продукции в отчетном периоде, тыс. руб. | Изменение цен в текущем
периоде по сравнению с
базисным, %
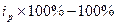
|
| Изделие 1 | +4,0 | ||
| Изделие 2 | +2,8 | ||
| Изделие 3 | -2,0 |
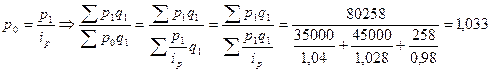
- средний гармонический индекс цен. Таким образом, цены в отчетном периоде по сравнению с базисным увеличились на 3,3%.
На основании имеющихся данных можно рассчитать индекс товарооборота:
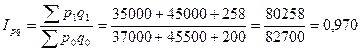
Общий товарооборот снизился на 3%.
Используя взаимосвязь между индексами, можно рассчитать индекс физического объема:
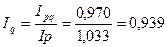
Результатом повышения цен явилось снижение объема продаж. Количество проданных изделий сократилось на 6,1%.
Пример расчета среднего арифметического индекса.
Имеются следующие данные о затратах на производство продукции (табл. 3). Как изменится объем произведенной продукции в стоимостном выражении?
Таблица 3
| Наименование продукции | Общие затраты на производство продукции в базисном периоде, тыс. руб. | Изменение физического объема произведенной продукции в отчетном периоде по сравнению с базисным, % |
| Изделие А | +2,5 | |
| Изделие В | +3,6 | |
| Изделие С | -2,1 |
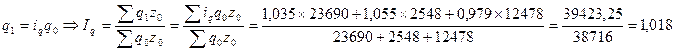 где z0, z1 - себестоимость единицы продукции в базисном и отчетном периоде соответственно.
где z0, z1 - себестоимость единицы продукции в базисном и отчетном периоде соответственно.
Физический объем произведенной продукции в целом по предприятию увеличился на 1,8%.
Дата добавления: 2016-12-16; просмотров: 2690;
