Задачи изучения взаимосвязей
Процесс статистического исследования взаимосвязей включает в себя три задачи:
— обнаружение зависимости и установление ее характера;
— оценка интенсивности связи;
— расчет прогнозных нормативных оценок показателей.
Интенсивность связи — характеризуется следующими показателями:
а) сила связи — характеризует степень влияния признака причины на признак-следствие (фактора на результат). Как правило, показатели силы связи характеризуют, насколько изменится результат, если фактор изменится на 1 (на 1%). Сила связи характеризует ее устойчивость;
б) теснота связи — это уровень согласованности (степень) изменения взаимодействующих признаков. Иногда показателям тесноты связи дают вероятностную характеристику (интерпретацию). А именно: теснота связи характеризует вероятность, с которой можно правильно предсказать значение у, зная значение х, то есть фактора, или это вероятность правильно предсказать изменение у, зная изменение х.
Расчет прогнозных, нормативных оценок показателейна основе проведенного измерения связей. Является практическим результатом решения двух первых задач.
Обнаружить связь между признаками — значит найти то или иное соответствие изменений одного ряда значений признака изменениям в ряде значений другого признака. Практически эта связь двух признаков обнаруживается сопоставлением соотношений между соответствующими парами значений признаков, а статистический ряд, образуемый этими парами, называют корреляционным рядом. Метод установления взаимосвязи при помощи сопоставления значений двух рядов называется методом параллельных рядов.
Для решения первой задачиможно воспользоваться следующими простыми методами:
— метод группировки;
— графический метод.
Например, если мы хотим выяснить, существует ли зависимость между количеством внесенных удобрений и урожайностью (цифры условные), скажем за 10 лет, то мы можем получить следующий корреляционный ряд (табл.1):
Таблица 1
| Годы | ||||||||||
| Признак х (количество внесенных удобрений на 1 га, кг.) | ||||||||||
| Признак у (урожайность, ц/га.) |
Чтобы сделать существование (или отсутствие) зависимости более наглядной, сгруппируем пары этого ряда так, чтобы объединить одинаковые значения признака, рассматриваемого в качестве фактора х (количество внесенных удобрений на 1 га) и рассчитать среднее по группе значение соответствующего признака-результата у (урожайность). Расположим пары значений в порядке убывания х (табл. 2):
Таблица 2
| Значения признака х (в порядке убывания) | Число лет с данным значением ЛС | у (средняя урожайность) |
После группировки отчетливо видно существование прямой зависимости между анализируемыми показателями: количество вносимых удобрений оказывает влияние на урожайность. Связь прямая.
Для обнаружения и статистического исследования зависимостей имеют значение все виды группировок: типологические, структурные, аналитические. Но наиболее часто используются аналитическая и типологическая группировки.
 Второй способ — графический, используется для установления зависимости по несгруппированным данным. Суть способа сводится к тому, что ряды показателей, между которыми ищется взаимосвязь, изображаются графически, и визуально устанавливается наличие связи между ними. Установление связи при помощи графического изображения имеет преимущество в том, что позволяет определить форму связи: прямолинейная или криволинейная.
Второй способ — графический, используется для установления зависимости по несгруппированным данным. Суть способа сводится к тому, что ряды показателей, между которыми ищется взаимосвязь, изображаются графически, и визуально устанавливается наличие связи между ними. Установление связи при помощи графического изображения имеет преимущество в том, что позволяет определить форму связи: прямолинейная или криволинейная.
 у
у
у - а + вх (прямая)
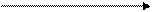 х
х
= ex' + ex + a, парабола
у = a +, гипербола x
Вторая задача решается по-разному в зависимости от того, между какими признаками устанавливается взаимосвязь (качественными или количественными). Оценка связи между количественными признаками осуществляется при помощи корреляционно-регрессионного анализа.
1.8.3. Понятие корреляционно-регрессионного анализа, условия его применения
Корреляционно-регрессионный анализ (КРА)— один из методов многомерного статистического анализа, в котором форма и интенсивность связи представлена в формализованном виде, то есть в виде математических уравнений и формул.
Применение КРА возможно при соблюдении следующих условий:
— должна быть достаточная численность наблюдений (как правило, считается, что число факторов должно быть меньше числа наблюдений в 6—8 раз);
— наблюдения должны быть статистически независимы;
— совокупность, по которой рассчитывается КРА, должна
быть однородна (подчиняться одному закону развития);
— должны быть количественные переменные.
Выполнение условий 1 - 4 необходимо для того, чтобы применять результаты КРА для прогнозных, нормативных, перспективных расчетов. В противном случае, результаты КРА применяются только для объяснения фактов.
Можно выделить две основные задачи КРА:
— оценка параметров уравнения регрессии, то есть уравнения, которое описывает взаимосвязь между фактором х и фактором у (задача регрессионного анализа);
— оценка тесноты связи (задача корреляционного анализа).
Для оценки параметров используется несколько методов математической статистики:
- наименьших квадратов;
- наименьших расстояний;
- избранных точек.
Рассмотрим технологию оценки параметров методом наименьших квадратов на простейшем случае: один фактор, один результат, связь прямая.
Метод наименьших квадратов:
Идея метода: теоретическая прямая строится таким образом, чтобы был минимум ∆: min ∆ = ∑(y - yx)2, где ух = а + вх.
 Решая относительно аи вэто уравнение, находим оценки параметров:
Решая относительно аи вэто уравнение, находим оценки параметров:
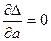
|
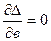
|
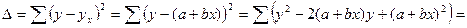
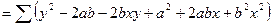
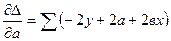
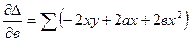
 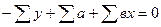
| , ∑a = na |
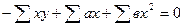
| |
 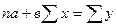
| |
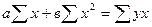
|
Решая систему линейных нормальных уравнений относительно с и в, получаем оценки параметров аи в, обеспечивающие min ∆
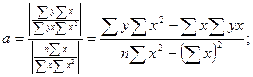
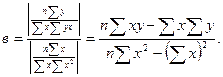
Пример оценки параметров уравнения регрессии.
Имеются данные о стаже и выработке (табл. 3, гр. 1 - 2):
| №п/п | Стаж, х | Месячная выработка, y | x 2 | xy | y 2 | yx | ( y- 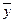 )2 )2
| ( yx- 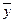 )2 )2
|
| А | ||||||||
| 4,0 | 16,00 | 880,0 | 266,06 | 5715,36 | 872,61 | |||
| 6,5 | 42,25 | 2015,0 | 282,90 | 207,36 | 161,29 | |||
| 4,2 | 17,64, | 1373,4 | 267,41 | 985,96 | 794,68 | |||
| 4,5 | 20,25 | 1237,5 | 269,43 | 424,36 | 684,87 | |||
| 6,0 | 36,00 | 1680,0 | 279,53 | 243,36 | 258,24 | |||
| 4,5 | 20,25 | 1138,5 | 269,43 | 1814,76 | 684,87 | |||
| 4,7 | 22,09 | 1151,5 | 270,77 | 2560,36 | 616,53 | |||
| 16,0 | 256,00 | 5440,0 | 346,88 | 1971,36 | 2629,64 | |||
| 13,2 | 174,24 | 4118,4 | 328,02 | 268,96 | 1051,06 | |||
| 14,0 | 196,00 | 4928,0 | 333,41 | 3180,96 | 1429,60 | |||
| 11,0 | 121,00 | 3575,0 | 313,21 | 864,36 | 310,11 | |||
| 12,0 | 144,00 | 3696,0 | 319,94 | 153,76 | 592,44 | |||
| Итого | 100,6 | 1065,72 | 31233,3 | - | 1532,58 | 10085,9 |
Постройте уравнение связи между стажем и месячной выработкой.
Определим параметры уравнения регрессии по приведенным выше формулам (промежуточные расчеты оформим в таблице 3 в графах 3 - 5).
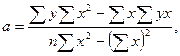
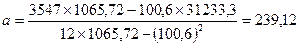
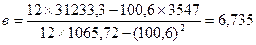
Таким образом, получилось уравнение регрессии: ух = 239,12+ 6,735х.
На основании полученного уравнения рассчитаем теоретические уровни признака у (по уравнению связи, подставляя в него значения признака х). Результаты расчетов занесем в таблицу 3, графа 6. Интерпретация полученных параметров:
Чаще всего, а не имеет экономической интерпретации. Иногда а показывает начальный уровень у, то есть значение у при х = 0.
Параметр в - сила связи, то есть увеличение стажа на 1 год в среднем приводит к увеличению выработки на 6,735 рублей.
Дата добавления: 2016-12-16; просмотров: 1865;
