Меры оценки тесноты связи для атрибутивных признаков
Для измерения связи между качественными(атрибутивными) признаками в статистике используются:
— коэффициент сопряженности А.А.Чупрова;
— коэффициент ассоциации К.Пирсона;
— коэффициенты ранговой корреляции Спирмена, Кендалла, Фехнера.
Применение первых двух показателей основано на построении таблиц сопряженности. Расчет этих показателей достаточно сложный и поэтому рассматриваться не будет, хотя дает наиболее точные измерения корреляционной зависимости.
Менее точные, но распространенные ввиду несложности применения, коэффициенты ранговой корреляции.
1. Коэффициент Фехнера рассчитывается на основе сравнения параллельных рядов, с его помощью можно установить направление связи и ее тесноту:
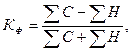
где ∑С — число совпадений знаков отклонения индивидуальных значений от средних значений признаков; ∑Н — число несовпадений.
2. Коэффициент корреляции Спирмена:
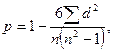
где d - разность рангов; n - число наблюдений.
Ранг - порядковый номер упорядоченного по убыванию или возрастанию ряда значений признака.
3. Коэффициент ранговой корреляции Кендалла:
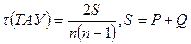
P и Q — определяются для неупорядоченного ряда (ряд результативного признака у);
Р равен сумме рангов, больших, чем взятый ранг (со знаком +);
Q равно сумме рангов, меньших, чем взятый ранг (со знаком -).
Пример расчета коэффициентов Фехнера, Спирмена, Кендалла.
В таблице 4 имеются два параллельных ряда преступлений и правонарушений. Предположим, что чем больше правонарушений, тем выше число преступлений, то есть число правонарушений является свидетельством более высокой преступности. Ряд числа правонарушений обозначим за х (фактор), а ряд числа преступлений за у (результат). Оценим взаимосвязь между признаками с помощью коэффициентов Фехнера, Спирмена и Кендалла.
Таблица 4
| № н/п | Правонарушения (jc) | Преступления (у) | По Фехнеру | По Спирмену | ||||
| знаки отклонения от средней | ранги по признакам | разность рангов | ||||||
| X | У | X | У | d | d2 | |||
| - | - | 4 j | ||||||
| - | - | |||||||
| - | - | 1. | ||||||
| + | + | |||||||
| + | - | |||||||
| + | + | |||||||
| + | + | |||||||
| 65,3 | 7,4 |
1. Рассчитаем коэффициент Фехнера:
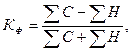
По данным таблицы 4 сравниваем 4 и 5 графы, в которых отражены знаки отклонений от средних, и считаем число совпадений знаков и несовпадений. Например, несовпадение знаков только в пятой строке, по всем остальным строкам знаки совпадают: либо оба положительные, либо отрицательные.

Коэффициент Фехнера изменяется от +1 до -1. Значение коэффициента близко к единице, что свидетельствует о существенной прямой согласованности в изменении признаков. Связь между числом правонарушений и числом преступлений сильная.
2. По данным таблицы 4 рассчитаем коэффициент Спирмена. Ряд х (правонарушения) проранжируем (упорядочим) по возрастанию (гр. 6), затем проставим ранги по ряду у, не меняя значения местами (гр. 7). Найдем разницу между рангами и возведем в квадрат (гр. 8, 9).
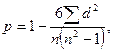

Расчет коэффициента Спирмена также подтверждает наличие сильной связи между признаками.
3. Рассчитаем коэффициент ранговой корреляции Кендалла по данным таблицы 4, расчет представим в таблице 5.
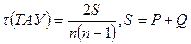
Р и Q — определяются для неупорядоченного ряда (в нашем случае это ряд у).
Р равен сумме ниже расположенных рангов, больших, чем взятый ранг (со знаком +), например: берем первый ранг - 3 и считаем, сколько расположенных ниже значений рангов превышают значение первого, равного 3, записываем в графе Р 4, берем следующий, равный 2, считаем нижние значения, превышающие 2, и т.д.
Q равно сумме рангов, меньших, чем взятый ниже ранг (со знаком -), рассчитываем аналогично:
Таблица 5
| № п/п | Ранг у | Р | Q | S | |
| -2 | |||||
| % | -1 | ||||
| . 5 | -1 | ||||
| Итого | - | - | - |
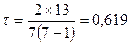
На основании коэффициента Кендалла можно сделать вывод об умеренной связи между признаками.
При расчете различных измерителей корреляционной связи на основании одних и тех же
данных мы получаем разные результаты. Это говорит не о том, что мы получили неверные результаты, а об условности измерителей.
По степени тесноты связи различают следующие количественные критерии оценки тесноты связи:
| Коэффициент корреляции | Характер связи |
| до 0,3 | практически отсутствует |
| 0,3—0,5 | слабая |
| 0,5—0,7 | умеренная |
| 0,7—1,0 | сильная |
Для таблиц сопряженности 2x2 (табл. 6) разработаны более простые меры связей, так называемые коэффициенты ассоциации и контингенции.
Таблица 6
| x1 | х2 | ||
| У1 | а | b | a+b |
| У2 | с | d | c+d |
| а+с | b+d | n=a+b+c+d |
В таблицах сопряженности 2x2 признак х и признак у принимает только по два значения. Коэффициент ассоциации:
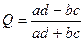 ,
,
Коэффициент контингенции:

Коэффициент контингенции дает более строгую оценку тесноты связи. Считается, что можно делать вывод о существовании связи между признаками, при коэффициенте ассоциации, равном 0,5, или коэффициенте контингенции, равном 0,3.
Пример расчета коэффициентов ассоциации и контингенции.
Для установления связи между полом и уровнем образования обследованы 60 мужчин и 60 женщин (табл. 7).
Таблица 7
| Пол/образование | Среднее и среднее специальное | Высшее | Итого |
| Женский | |||
| Мужской | |||
| Всего |
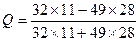
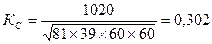
На основании коэффициентов делаем вывод о существовании связи между уровнем образования и полом.
В заключение следует обратить внимание, что нельзя даже самые точные расчеты абсолютизировать, так как даже самый высокий коэффициент корреляции еще ничего не говорит о действительной причинной связи между явлениями. Их расчет является лишь лишним подтверждением наличия связи, вывод о которой делается на уровне теоретического, качественного анализа.
Выводы:
1. Изучение взаимосвязей между явлениями позволяет не только объяснить изменения, исходящие в одних явлениях под влиянием других, но и дает возможность управлять процессами, зная механизм их взаимодействия.
2. Как правило, в статистике изучается стохастическая зависимость, то есть зависимость, которая проявляется в большинстве случаев, а не в каждом единичном случае.
3. Конечной целью изучения взаимосвязей является прогнозная оценка развития явления. Оценка силы и тесноты связи между количественными признаками осуществляется помощи корреляционно-регрессионного анализа.
4. Оценка связи между качественными признаками осуществляется при помощи непараметрических мер связей, основанных на таблицах сопряженности.
Дата добавления: 2016-12-16; просмотров: 1366;
