Средняя и предельная ошибки выборки
Основное преимущество выборочного наблюдения среди прочих других — возможность рассчитать случайную ошибку выборки.
Ошибки выборки бывают систематические и случайные.
Систематические— в том случае, когда нарушен основной принцип выборки — случайности. Случайные— возникают обычно ввиду того, что структура выборочной совокупности всегда отличается от структуры генеральной совокупности, как бы правильно ни был произведен отбор, то есть, несмотря на принцип случайности отбора единиц совокупности, все же имеются расхождения между характеристиками выборочной и генеральной совокупности. Изучение и измерение случайных ошибок репрезентативности и является основной задачей выборочного метода.
Как правило, чаще всего рассчитывают ошибку средней и ошибку доли. При расчетах используются следующие условные обозначения:
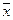 — средняя, рассчитанная в пределах генеральной совокупности;
— средняя, рассчитанная в пределах генеральной совокупности;
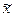 — средняя, рассчитанная в пределах выборочной совокупности;
— средняя, рассчитанная в пределах выборочной совокупности;
р — доля данной группы в генеральной совокупности;
w — доля данной группы в выборочной совокупности.
Используя условные обозначения, ошибки выборки для средней и для доли можно записать следующим образом:
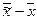
w- р.
Выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать любые значения в зависимости от того, какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок μ.
В отличие от систематической, случайную ошибку можно определить заранее, до проведения выборки, согласно предельных теорем, рассматриваемых в математической статистике.
Средняя ошибка определяется с вероятностью 0,683. В случае другой вероятности говорят о предельной ошибке.
Средняя ошибка выборки для средней и для доли определяется следующим образом:
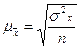

В этих формулах дисперсия признака является характеристикой генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными xapaктеристиками выборочной совокупности на основании закона больших чисел, по которому выборочная совокупность большом объеме точно воспроизводит характеристики генеральной совокупности.
Формулы определения средней ошибки для различных способ отбора:
| Способ отбора | Повторный | Бесповторный | ||
| ошибка средней | ошибка доли | ошибка средней | ошибка доли | |
| Собственно-случайный и механический | 
| 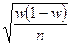
| 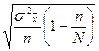
| 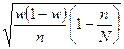
|
| Типический | 
| 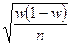
| 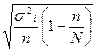
| 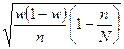
|
| Серийный | 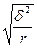
| 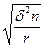
| 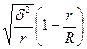
| 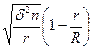
|
μ - средняя ошибка;
∆ - предельная ошибка;
п - численность выборки;
N - численность генеральной совокупности;
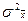 - общая дисперсия;
- общая дисперсия;
w - доля данной категории в общей численности выборки:
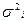 - средняя из внутригрупповых дисперсии;
- средняя из внутригрупповых дисперсии;
Δ2 - межгрупповая дисперсия;
r - число серий в выборке;
R — общее число серий.
Предельная ошибкадля всех способов отбора связана со средней ошибкой выборки следующим образом:
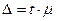
где t - коэффициент доверия, функционально связанный с вероятностью, с которой обеспечивается величина предельной ошибки. В зависимости от вероятности коэффициент доверия t принимает следующие значения:
| t | P |
| 0,683 | |
| 1,5 | 0,866 |
| 2,0 | 0,954 |
| 2,5 | 0,988 |
| 3,0 | 0,997 |
| 4,0 | 0,9999 |
Например, вероятность ошибки равна 0,683. Это значит, что генеральная средняя отличается от выборочной средней по абсолютной величине не более чем на величину μ с вероятностью 0,683, то если 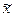 - выборочная средняя,
- выборочная средняя, 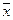 - генеральная средняя, то
- генеральная средняя, то 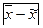 с вероятностью 0,683.
с вероятностью 0,683.
Если мы хотим обеспечить большую вероятность выводов, тем самым мы увеличиваем границы случайной ошибки.
Таким образом, величина предельной ошибки зависит от следующих величин:
- колеблемости признака (прямая связь), которую характеризует величина дисперсии;
- численности выборки (обратная связь);
- доверительной вероятности (прямая связь);
- метода отбора.
Пример расчета ошибки средней и ошибки доли.
Для определения среднего числа детей в семье методом случайной бесповторной выборки из 1000 семей отобраны 100. Результаты приведены в таблице:
| Число детей, чел. | Число семей |
| Итого |
Определите: .
— с вероятностью 0,997 предельную ошибку выборки и границы, в которых находится средне число детей в семье;
— с вероятностью 0,954 границы, в которых находится удельный вес семей с двумя детьми.
1. Определим предельную ошибку средней с вероятностью 0,977. Для упрощения расчетов воспользуемся способом моментов:
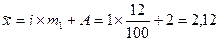
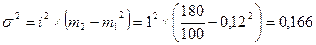

 p = 0,997 t = 3
p = 0,997 t = 3
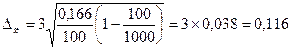
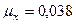
средняя ошибка средней, 0,116 — предельная ошибка
2,12 – 0,116 ≤ 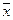 ≤ 2,12+ 0,116
≤ 2,12+ 0,116
2,004 ≤ 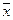 ≤ 2,236
≤ 2,236
Следовательно, с вероятностью 0,997 среднее число детей в семье в генеральной совокупности, то есть среди 1000 семей, находится в интервале 2,004 — 2,236.
2. Определим предельную ошибку доли с вероятностью 0,954.

 p = 0,954 t = 2
p = 0,954 t = 2
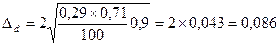
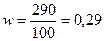
29 - 8,6 ≤ d ≤ 29 +8,6
20,4% < d < 37,6%
Доля семей с двумя детьми в общей численности семей от 20,4% до 37,6%, или число их от 201 до 376 человек.
Помимо прямой задачи (определение величины ошибки) фор предельной ошибки позволяет решать еще две задачи.
Определить необходимую численность выборки, при которой пределы возможной ошибки не превышают некоторой за величины.
Определить вероятность того, что в проведенной выборке ошибка будет заключаться в заданных пределах.
Решение этих задач зависит от способа отбора. Например, необходимая численность выборки для повторного отбора:
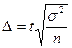


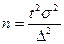
при без повторной:
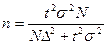
Пример расчета численности выборки при заданных параметрах. Нужно определить среднее число рабочих 3 разряда. Найти численность выборки n, чтобы с вероятностью 0,954 ошибка не превышала бы 0,02, если известно, что σ2 = 0,2, а общая численность рабочих 10000 чел. Р = 0,954,значит t = 2
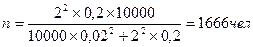 .
.
Дата добавления: 2016-12-16; просмотров: 7975;
