Показатели тесноты связи, линейный коэффициент корреляции

Теснота связиоценивается при помощи следующих показателей: — эмпирическое корреляционное отношение. Этот показатель используется для оценки тесноты связи по аналитической груп­пировке и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии (см. тему «Показа­тели вариации»);

- теоретическое корреляционное отношение (индекс корре­ляции). Этот показатель рассчитывается по уравнению связи. Применяется следующая формула:

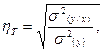
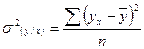- факторная дисперсия (объясненная связью с фактором х дисперсия результативного признака у).

Теоретическое корреляционное отношение характеризует долю общей вариации результативного признака, объясняемую на основе выбранно­го уравнения связи результативного и факторного признаков.

Индекс корреляции изменяется в пределах: 0 ≤ η_Т ≤ 1

В том случае, если η_Т = 0, связи между переменными нет. Приме­няется условная шкала для оценки тесноты связи: до 0,3 — слабая связь; 0,3 - 0,7 — средняя (умеренная); 0,7 - 1,0 — сильная связь.

Пример расчета теоретического корреляционного отношения (по данным таблицы 3).

Произведем необходимые расчеты (табл.3, гр. 7-8).

Факторная дисперсия:

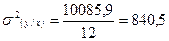
Общая дисперсия результативного признака у:

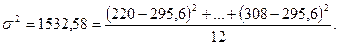
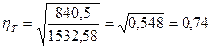
На основании произведенных расчетов можно сделать вывод, что связь между стажем и выработке сильная.

Перечисленные показатели тесноты связи могут быть использованы как при парной, так и в случае множественной регрессии.

При линейной форме зависимости для оценки тесноты связи можно воспользоваться линейным коэффициентом корреляции (ЛКК), который был предложен английским статистиком К.Пирсоном, пользуется несколько его формул:

1.

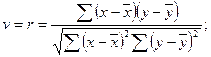
2.

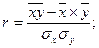
3. .

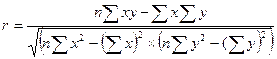Пример расчета линейного коэффициента корреляции.

Рассчитаем по данным таблицы 3 линейный коэффициент корреляции (зависимость линейная). Удобнее всего воспользоваться третьим вариантом формулы и использовать результаты предыдущих расчетов (табл. 3, итоги гр. 1 - 5).

Индекскорреляции и линейный коэффициент ее показывают тесную связь между стажем работы и выработкой.

Свойства линейного коэффициента корреляции:

- измеряет тесноту линейной связи. Иначе, значение r = 0 не дает оснований говорить о том, что
между переменными отсутствует связь, r = 0 показывает отсутствие линейной связи;

- является величиной безразмерной, что позволяет сравнивать между собой различные статистические ряды;

- r изменяется от -1 до 1:

r = -1 — полная, обратная, линейная связь;

r = 1 — полная, прямая, линейная связь;

— шкала та же, что и для индекса, но с модулем r.
Замечания:

Взаимосвязь между коэффициентом регрессии и линейным коэффициентом корреляции:

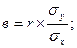
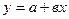
Для проверки линейности связи между переменными можно использовать соотношение:

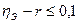
В случае линейной связи: .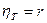

Результаты расчетов по данным таблицы 3 теоретического корреляционного отношения и ли­нейного коэффициента корреляции очень близки между собой, что подтверждает, что связь между стажем и выработкой линейная. Положительное значение линейного коэффициента корреляции сви­детельствует, что связь прямая, то есть с увеличением стажа увеличивается выработка.