Абсолютные и относительные ошибки

Такие ошибки, как средняя (J), средняя квадратическая (m), вероятная (r), истинная (D) и предельная (D_пр), являются абсолютными ошибками. Они всегда выражены в единицах измеряемой величины, т.е. имеют одинаковую с измеряемой величиной размерность.
Часто возникают случаи, когда разные по величине объекты измеряют с одинаковыми абсолютными ошибками. Например, средняя квадратическая ошибка измерения линий длиной: l₁ = 100 м и l₂ = 1000 м, составила m = 5 см. Возникает вопрос: какая же линия измерялась точнее ? Чтобы избежать неопределенности, точность измерений ряда величин оценивают в виде отношения абсолютной ошибки к значению измеряемой величины. Полученное отношение называется относительной ошибкой, которую обычно выражают дробью с числителем, равным единице.
Наименование абсолютной ошибки определяет и название соответствующей ей относительной ошибки измерения [ 1 ].

Пусть x - результат измерения некоторой величины. Тогда
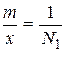- cредняя квадратическая относительная ошибка;

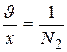- средняя относительная ошибка;

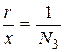- вероятная относительная ошибка;

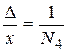- истинная относительная ошибка;

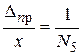- предельная относительная ошибка.

Знаменатель N относительной ошибки необходимо округлять до двух значащих цифр с нулями:

m_x = 0,3 м; x = 152,0 м;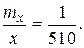

m_x = 0,25 м; x = 643,00 м; .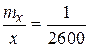

m_x = 0,033 м; x = 795,000 м;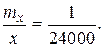

Как видно из примера, чем больше знаменатель дроби, тем точнее выполнены измерения.

Ошибки округления

При обработке результатов измерений немаловажную роль играют ошибки округления, которые по своим свойствам можно отнести к случайным величинам [ 2 ]:

1) предельная ошибка одного округления составляет 0,5 единицы удерживаемого знака;

2) большие и меньшие по абсолютной величине ошибки округления равновозможны;
3) положительные и отрицательные ошибки округления равновозможны;
4) математическое ожидание ошибок округления равно нулю.
Эти свойства позволяют отнести ошибки округления к случайным величинам, имеющим равномерное распределение. Непрерывная случайная величина X имеет равномерное распределение на интервале [a, b], если на этом интервале плотность распределения случайной величины постоянна, а вне его равна нулю (рис. 2), т.е.

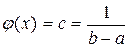j (x ) . (1.32)

Функция распределения F(x)

с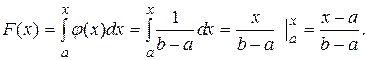

a b x (1.33)

Рис. 2 Математическое ожидание

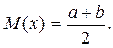(1.34)

Дисперсия
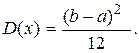(1.35)

Среднее квадратическое отклонение

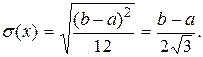(1.36)

Для ошибок округления

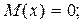
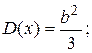
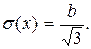(1.37)

Следовательно, средняя квадратическая ошибка округления m_о вычислится согласно

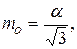
(1.38)

где a = 0,5.

Подставляя это значение в равенство (1.38), получим

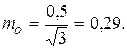
Как видно из примера, m_c незначительно отличается от ошибки измерения m.

В вычислительной практике для уменьшения влияния ошибок округления промежуточные результаты принимают на порядок выше результатов измерения. Например, если результаты линейных измерений имеют ошибку 1 мм, то промежуточные значения определяют с точностью до 0,1 мм.