Меры точности результатов измерений

Для оценки точности отдельного измерения некоторой величины необходимо определить возможные отклонения результатов измерения этой величины от ее истинного значения. Суждение о точности выполненных измерений можно получить по степени различия результатов измерений в ряду: чем больше разбросаны результаты в ряду, тем сильнее рассеивание (дисперсия) ряда, тем менее точны измерения.

Возьмем два ряда измерений, выполненных в различных условиях, истинные ошибки которых будут:

-3, +2, +4, -2, -1, 0, +4, -3, +2, -3;
0, -1, +7, +2, -1, -1, -8, 0, +3, -1.

Сопоставляя ряды, видим, что разброс ошибок во втором ряду больше, чем в первом. Следовательно, условия измерений в первом случае более благоприятны.

Найдем среднюю ошибку, которая определяется по абсолютным значениям ошибок ряда

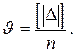(1.12)

В результате вычислений получим следующие значения средних ошибок J₁ = 2,4; J₂ = 2,4. Как видим, оба значения одинаковы. Это объясняется тем, что J недостаточно чувствительно к наличию крупных ошибок.
В качестве меры точности Гаусс предложил принять среднее квадратическое отклонение или среднюю квадратическую ошибку согласно равенству (1.5)

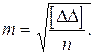(1.13)

Вся теория математической обработки результатов измерений построена на использовании средней квадратической ошибки, которая обладает рядом преимуществ:

1) при вычислении нет необходимости учитывать знак величины D_i отдельных ошибок;

2) большие по абсолютному значению величины D_i после возведения в степень увеличивают ее численные значения, создавая своего рода “запас прочности”;

3) по формуле (1.13) значение средней квадратической ошибки m получается со знаком “ ± “, что соответствует природе случайных ошибок.
Отличием средней квадратической ошибки m от стандарта s является то, что средняя квадратическая ошибка - величина эмпирическая, вычисляемая из ограниченного числа измерений, а стандарт - величина постоянная, характеризующая бесконечную совокупность данного вида измерений. Это - величина теоретическая. При n ® ¥ , m ® s. Для нашего примера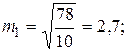

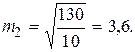
Из сравнения m₁ и m₂ cледует, что условия измерений для первого ряда лучше, чем для второго ряда.

Так как s всегда остается неизвестным, то приходится пользоваться его “оценкой” m, т.е. m » s, которое в свою очередь определяется с ошибкой m_m

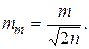(1.14)

Cуществует связь между средней и средней квадратической ошибками при n ® ¥

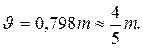(1.15)

Иногда в качестве меры точности используют вероятную ошибку r, которая делит ряд ошибок, расположенных в порядке возрастания их абсолютных значений, пополам. При n ® ¥ вероятная ошибка r связана со средней квадратической ошибкой зависимостью

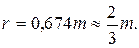(1.16)