Свойства случайных ошибок

Случайные ошибки измерений подчиняются нормальному закону распределения с плотностью

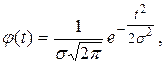
(1.2)
где t - текущее значение случайной ошибки измерений;
s - среднее квадратическое отклонение (стандарт) генеральной совокупности этих ошибок.

Из анализа функции (1.2) имеем:

1) функция достигает максимальных значений при t = 0;

2) функция четная, т.е. f(t) = f(-t); отсюда следует, что кривая симметрична относительно значения t = 0;

3) математическое ожидание случайных ошибок измерений определится согласно

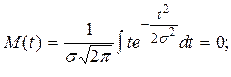(1.3)

4) дисперсия случайных ошибок измерений запишется в виде

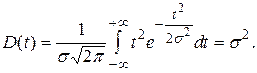
(1.4)

Отсюда среднее квадратическое отклонение

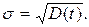(1.5)

Равенство (1.2) носит название уравнения кривой Гаусса. Свойства ее совпадают с кривой нормального распределения (рис.1). Отсюда получим следующие свойства случайных ошибок измерений.

1. При данных условиях измерений случайные ошибки не могут превзойти по абсолютной величине определенного предела, т.е.

j ( t ) ½D½ = D_пр= 3s . (1.6)

2. Малые по абсолютной величине

ошибки встречаются чаще, чем

большие.
3. Положительные ошибки появляются

так же часто, как и равные им по

абсолютной величине отрицательные

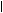
ошибки, т.е.

-3s -2s -s 0 s 2s 3s t p (D < 0) = p ( D > 0) = 0,5. (1.7)

Рис. 1

4. Среднее арифметическое из случайных ошибок измерений одной и той же величины стремится к нулю при неограниченном возрастании числа измерений, т.е.

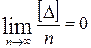. (1.8)

Если 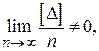то в этом случае систематическое влияние полностью не исключено.