Ошибки функций измеренных величин

В общем случае найдем среднюю квадратическую ошибку M_F некоторой функции вида

F = f (x₁ , x₂, . . . , x_n ), (1.39)

где x_i - коррелированные аргументы, связанные между собой зависимостями и полученные из наблюдений.

При этом будем иметь в виду, что средние квадратические ошибки результатов измерений m₁, m₂, . . . , m_n известны. Кроме этого, предположим, что X₁, X₂, . . . , X_n - истинные значения аргументов. Каждая величина измерялась k раз, т. е.

для X₁ : x₁₁, x₁₂, . . . , x_1k ;

для X₂ : x₂₁, x₂₂, . . . , x_2k;

. . . . . . . . . . . . . . . .

для X_n : x_n1, x_n2, . . . , x_nk.

Для каждой серии наблюдений получим значения оцениваемой функции (1.39):

F₁= f ( x₁₁, x₁₂, . . . , x_1n ) ;

F₂ = f ( x₂₁, x₂₂, . . . , x_2n ) ;

. . . . . . . . . . . . . . . . . . . . . . (1.40)

F_k = f ( x_k1, x_k2, . . . , x_kn ) .

Используя равенство (1.1), получим вместо уравнений (1.40) следующие зависимости:

F₁ = f ( X₁ + D ₁₁, X₂ + D₂₁, . . . , X_n + D_n1 ) ;

F₂ = f ( X₁ + D₁₂, X₂ + D₂₂, . . . , X_n + D_n2 ) ; (1.41)

. . . . . . . . . . . . . . . . . . . . . . . . .

F_k = f ( X₁ + D_1k, X₂ + D_2k, . . . , X_n + D_nk ) .

Разложив равенства (1.41) в ряд Тейлора и ограничиваясь в виду малости ошибок измерений первыми степенями разложения, получим

F₁ = f ( X₁, X_2,..., X_n ) +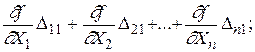

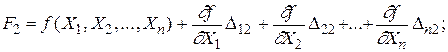(1.42)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

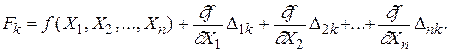Учитывая, что истинная ошибка функции

,

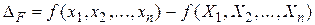получим систему случайных ошибок функций независимых величин

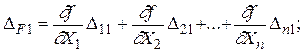
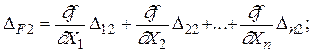(1.43)

. . . . . . . . . . . . . . . . . . . . . . .

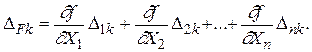
Возведя каждое равенство системы (1.43) в квадрат, просуммировав полученные значения и разделив их на k, придем к следующему уравнению:

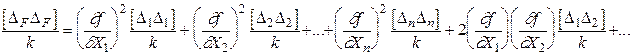
(1.44)

В математической статистике доказывается следующая теорема [ 2 ]: “Среднее значение произведения случайных величин равно произведению средних значений сомножителей”

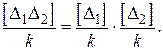(1.45)

Согласно четвертому свойству случайных ошибок каждое из сомножителей равенства (1.45) стремится к нулю при неограниченном возрастании числа измерений. Поэтому можно утверждать, что и

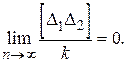(1.46)

Перейдем к средним квадратическим ошибка функции независимых величин, учитывая равенство (1.13), а также условие (1.46)
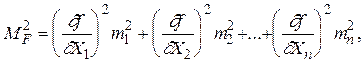(1.47)

где m_l - cредние квадратические ошибки измеренных величин.

Если аргументы зависимы (коррелированы), то для средних значений произведений ошибок этих величин при k ® ¥ справедливо равенство [ 1 ]

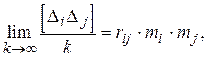(1.48)

где r_ij - коэффициент корреляции между зависимыми аргументами.
C учетом равенства (1.48) выражение (1.44) примет следующий вид 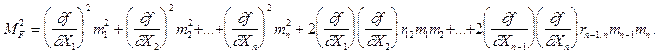(1.49)

Типовые примеры