Анализ результатов опытно-экспериментального исследования

На констатирующем этапе, исследование с помощью выбранных методик нами было сделано ……позволило получить показатели уровня овладения логическими операциями, развития знаний о составе числа первого десятка, умений считать в пределах десяти и пользоваться количественными и порядковыми числительными, а также уровня развития представлений о числах у детей старшего дошкольного возраста в экспериментальной и контрольной группах.

Полученные нами начальные результаты обследования развития логического мышления по методике «Самое непохожее» Л.А. Венгера приведены в Приложении 4 (Таблица 1) на рисунке 2.1. Констатирующая диагностика уровня овладения операциями анализа, синтеза, сравнения и обобщения показала:

- в экспериментальной группе средний уровень овладения логическими операциями у 16 (70%) детей, низкий уровень у 7 (30%) детей;

- в контрольной группе средний уровень показали 15 (65%) детей, низкий уровень - 8 (35%) детей.

Проведение диагностической беседы «Самое непохожее» Л.А. Венгера показало, что у большинство детей в обеих группах слабо развиты умения определять различия и сходства геометрических фигур, почти все дети нашли отличающуюся от остальных геометрическую фигуру, но без помощи воспитателя не смогли назвать все ее существенные отличия.

В двух группах некоторые дети не смогли выполнить часть заданий самостоятельно без помощи воспитателя. Некоторые из детей в двух группах не смогли найти фигуру, которая отличается от других и назвать ее существенные отличия двух разных фигур. Мы также установили, что многие дети не могут определить такие отличия геометрических фигур как число сторон и углов, верно посчитать углы и стороны у геометрических фигур.

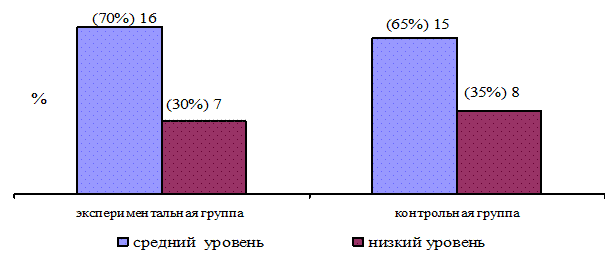
Рис. 2.1. Результаты диагностической беседы «Самое непохожее» Л.А. Венгера на констатирующем этапе

Рисунок 2.1. показывает, что на констатирующем этапе исследования показатели овладения логическими операциями в экспериментальной и контрольной группах находится на среднем и низком уровнях.

Отсутствие различия показателей уровня овладения логическими операциями детьми экспериментальной и контрольной групп на констатирующем этапе было доказано при помощи t-критерия Стьюдента. Его значение равно 0. В Приложении 5 (Таблица 1) приведен расчет t-критерия Стьюдента для данных показателей в экспериментальной и контрольной группах на констатирующем этапе.

Проведение тестирования по методике «Что будет, если…» С.Е. Гавриной показало результаты, которые представлены в Приложении 4 (Таблица 2) и на рисунке 2.2.

Обследование уровня развития знаний ребенка старшего дошкольного возраста о составе числа первого десятка (из отдельных единиц) на констатирующем этапе показала:

- в экспериментальной группе средний уровень знаний о составе числа первого десятка показали 14 (60%) детей, низкий уровень у 9 (40%) детей.

- в контрольной группе детей со средним уровнем развития знаний о составе числа 13 (57%), с низким уровнем развития 10 (43%) детей.

В ходе тестирования по методике «Что будет, если…» С.Е. Гавриной большинство детей в двух группах затруднялись при выполнении почти всех заданий на прибавление и сложение чисел, не могли выполнить задание на получение числа путем вычитания единицы из следующего за ним в ряду.

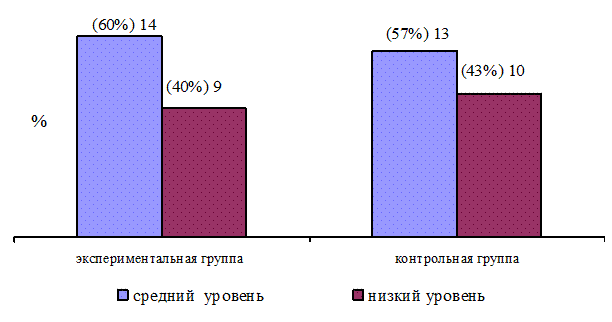
Рис. 2.2. Результаты тестирования по методике «Что будет если…» С.Е. Гавриной на констатирующем этапе

На рисунке 2.2 можно видеть, что на констатирующем этапе показатели развития знаний о составе числа первого десятка в экспериментальной и контрольной группах находятся на среднем и низком уровне. С помощью метода t-критерия Стьюдента доказано отсутствие различия показателей уровня развития знаний о составе числа первого десятка у детей экспериментальной и контрольной групп на констатирующем этапе. Значение t-критерия Стьюдента равно 0. В Приложении 5 (Таблица 2) приведен расчет t-критерия Стьюдента для показателей знаний о составе числа первого десятка в экспериментальной и контрольной группах на констатирующем этапе.

Результаты проведения констатирующей диагностики с помощью теста «Скажи сколько» Е.В. Колесниковой показаны в Приложении 4 (Таблица 3) и на рисунке 2.3.

Диагностика развития умения считать в пределах 10 и умения пользоваться количественными и порядковыми числительными на констатирующем этапе показала:

- в экспериментальной группе средний уровень развития счета и использования количественных и порядковых числительных обнаружен у 13 (57%), низкий уровень выявлен у 10 (43%) детей;

- в контрольной группе средний уровень показали 15 (65%), низкий уровень 8 (34%) детей.

Во время проведения тестирования по методике «Скажи, сколько?» Е.В. Колесниковой многие дети в двух группах допускали ошибки при счете (отсчитывании) предметов в пределах 10, неуверенно пользовались количественными числительными (не могли назвать точно количество предметов, неверно использовали слова, или совсем не могли назвать слово). Многие дети понимали вопрос «Сколько?», но неуверенно отвечали на него. Допускали ошибки при ответе на вопрос «Который по счету?».

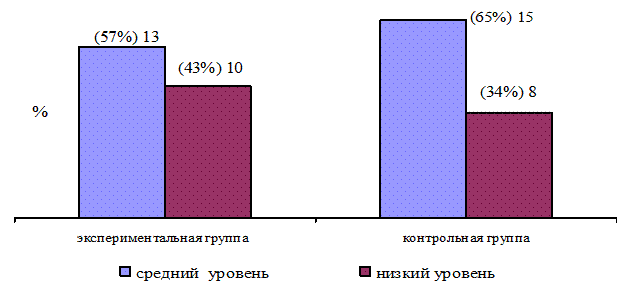
Рис. 2.3. Результаты тестирования по методике «Скажи, сколько?» Е.В. Колесниковой на констатирующем этапе

На рисунке 2.3 можно отметить, что на констатирующем этапе показатели развития умения считать в пределах 10, пользоваться количественными и порядковыми числительными в экспериментальной и контрольной группах находится на среднем и низком уровнях.

Для показателей, полученных по методике Е.В. Колесниковой значение критерия равно 0,1. Это говорит об отсутствии статистически значимых различий между показателями развития умения считать, пользоваться количественными и порядковыми числительными в экспериментальной и контрольной группах. В Приложении 5 (Таблица 3) приведен расчет t-критерия Стьюдента для показателей по методике Е.В. Колесниковой в экспериментальной и контрольной группах на констатирующем этапе.

Результаты тестирования по методике «Какой цифры не стало» Е.А. Носовой показаны в Приложении 4 (Таблица 4) и на рисунке 2.4.

Диагностика развития уровня представлений о числах на констатирующем этапе показала:

- в экспериментальной группе средний уровень развития представлений о числах определен 15 (65%), низкий уровень у 8 (34%) детей;

- в контрольной группе средний уровень определили у 17 (74%), низкий уровень 6 (26%) детей.

Во время проведения тестирования по методике «Какой цифры не стало» В.П. Новиковой мы обнаружили, что в обеих группах дети ошибаются при определении изменения в ряду цифр, многие дети не могли верно назвать порядок расположения цифр.

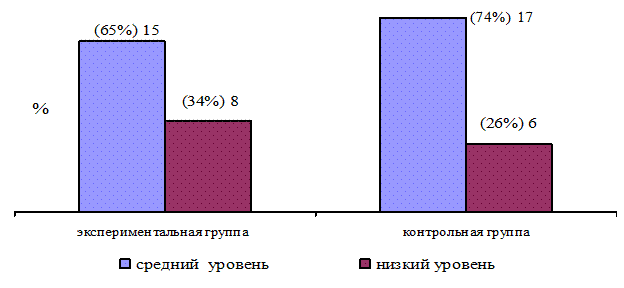
Рис. 2.4. Результаты тестирования по методике «Скажи, сколько?» Е.А. Носовой на констатирующем этапе

На рисунке можно отметить, что на констатирующем этапе показатели развития умения считать в пределах 10, пользоваться количественными и порядковыми числительными в экспериментальной и контрольной группах находится на среднем и низком уровнях.

В результате сравнения показателей, полученных по методике Е.А. Носовой с помощью метода t-критерия Стьюдента, было получено значение критерия равное 0,1. Это является доказательством отсутствия статистически незначимых различий между показателями развития представлений о числе в экспериментальной и контрольной группах на констатирующем этапе. В Приложении 5 (Таблица 4) приведен расчет t-критерия Стьюдента для показателей развития представлений о числе в экспериментальной и контрольной группах на констатирующем этапе.

Констатирующее исследование также показало, что проводимая воспитателями работа по формированию количественных представлений в экспериментальной и контрольной группах имеет существенные недостатки: недостаточный объем использования форм и методов работы по развитию вычислительной деятельности детей, отсутствие включения средств логического мышления, недостатки обновления дидактических, наглядных материалов для развития количественных представлений. Недостатками организации работы по формированию количественных представлений является в оформление предметно-пространственной среды: отсутствие доступных материалов, устаревшие игры и средства для самостоятельной счетной деятельности детей, недостаточное количество настольных математических и логических игр для развития счета, представлений о числе, развития логических операций.

Таким образом, на констатирующем этапе исследования с помощью диагностических бесед и тестирования были получены показатели овладения логическими операциями, развития знаний о составе числа первого десятка, умений считать в пределах 10 и пользоваться количественными и порядковыми числительными, а также уровня развития представлений о числах в экспериментальной и контрольной группах. В обеих группах показатели развития логического мышления и количественных представлений находятся на среднем и низком уровнях. Математико-статистическая обработка позволила установить отсутствие значимого отличия показателей развития логических операций и количественных представлений у детей экспериментальной и контрольной групп на констатирующем этапе. Результаты констатирующего этапа их обработка позволили нам перейти к формирующему этапу исследования.

После проведения формирующего этапа исследования по формированию количественных представлений у детей экспериментальной группы средствами логического мышления, мы приступили к контрольному обследованию по выше описанным методикам. В экспериментальной и контрольной группах, были вторично проведены диагностическая беседа и тестирование.

В результате повторного проведения диагностической беседы «Самое непохожее» Л.А. Венгера были получены показатели, которые представлены в Приложении 7 (Таблица 1). Сравнение показателей уровня освоения логических операций на констатирующем и контрольном этапах наглядно показаны на рисунке 2.5.

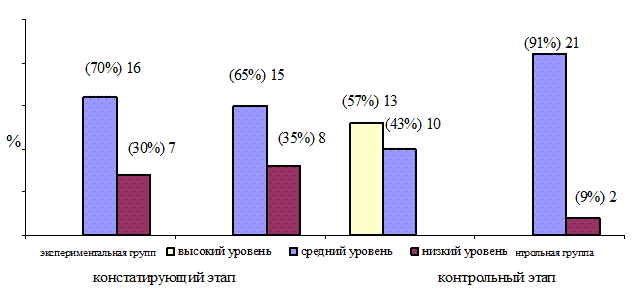
Рис. 2.5. Сравнение результатов диагностики по методике «Самое непохожее» Л.А. Венгера на констатирующем и контрольном этапах

На рисунке 2.5. видно, что на контрольном этапе исследования уровень развития мелкой моторики в экспериментальной группе значительно отличается от уровня развития в контрольной группе. Анализ результатов обследования логического мышления и количественных представлений полученных на констатирующем и контрольном этапах показал следующее. На констатирующем этапе высокий уровень овладения логическими операциями в экспериментальной группе не показал ни один из детей, средний уровень показали 16 (70%) детей; низкий уровень 7 (30%) детей. На контрольном этапе в экспериментальной группе показатели явно улучшились: высокий уровень диагностирован у 13 (57%) детей; средний уровень показали 10 (43%) детей; низкий уровень овладения логическими операциями не показал ни один из детей.

В контрольной группе явных изменений уровня овладения логическими операциями на констатирующем и контрольном этапах не выявлено. На констатирующем этапе в данной группе высокий не определился ни у одного из детей, средний уровень были диагностирован у 15 (65%) детей, низкий - у 8 (35%) детей. На контрольном этапе средний уровень показали 21 (91%) детей, низкий 2 (9%) детей.

Проводя методику «Самое непохожее» Л.А. Венгерамы отметили, что большинство детей в экспериментальной группе показали достаточное развитые умения определять различия и сходства геометрических фигур, дети безошибочно находят отличающуюся от остальных геометрическую фигуру, без помощи воспитателя могут назвать все ее существенные отличия от двух разных фигур, верно называя число сторон и углов, не допуская ошибок могут посчитать углы и стороны у геометрических фигур.

В контрольной группе у детей по-прежнему при выполнении заданий методики «Самое непохожее» Л.А. Венгераобнаружились слабыеумения определять различия и сходства геометрических фигур. Дети могут находить отличающуюся от остальных геометрическую фигуру, но большинство из них самостоятельно назвать все ее существенные отличия не смогли, с трудом назвали отличия геометрических фигур (число сторон и углов), допускали ошибки при подсчете углов и сторон у геометрических фигур.

Для сравнения показателей овладения логическими операциями на констатирующем и контрольном этапах исследования использовался метод t-критерия Стьюдента для зависимых выборок (Приложение 8, Таблица 1).

В экспериментальной группе значение t-критерия Стьюдента равно 2,3. полученное значение позволяет сделать вывод о существовании статистически значимого различия между показателями овладения логическими операциями у детей в экспериментальной группе на констатирующем и контрольном этапах. В контрольной группе было получено значение t-критерия Стьюдента равное 0,2. Это доказывает отсутствие различия между показателями овладения логическими операциями в контрольной группе на констатирующем и контрольном этапах (Приложение 9, Таблица 1).

Повторное тестирование по методике «Что будет, если…» С.Е. Гавриной позволило получить результаты, которые представлены в Приложении 7 (Таблица 2). Сравнение показателей развития знаний о составе числа первого десятка на констатирующем и контрольном этапах наглядно отражены на рисунке 2.6.

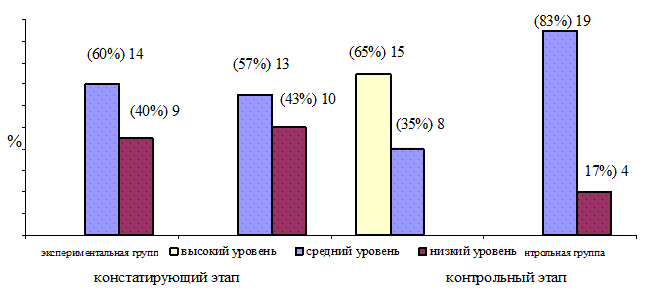
Рис. 2.6. Сравнение результатов диагностики по методике «Что будет если…» С.Е. Гавриной на констатирующем и контрольном этапах

Рисунок 2.6. демонстрирует, что на контрольном этапе исследования показатели знаний о составе числа первого десятка в экспериментальной и контрольной группах значительно отличаются. В экспериментальной группе показатели развития знаний о составе числа первого десятка значительно улучшились.

Анализ результатов обследования по методике «Что будет если…» С.Е. Гавриной позволил сделать следующие выводы. На констатирующем этапе в экспериментальной группе высокий уровень знаний о составе числа первого десятка выявлен не был, средний уровень показали 14 (60%) детей; низкий уровень 9 (40%) детей. На контрольном этапе в экспериментальной группе было обнаружено явное улучшение знаний о составе числа первого десятка: высокий уровень показали 15 (65%) детей; средний уровень показали 8 (35%) детей; низкий уровень знаний о составе числа первого десятка не выявлен.

В контрольной группе уровень овладения логическими операциями на констатирующем и контрольном этапах остался прежним. На констатирующем этапе в данной группе высокий уровень знаний о составе числа первого десятка не показал ни один из детей, средний уровень были диагностирован у 13 (57%) детей, низкий - у 10 (43%) детей. На контрольном этапе средний уровень знаний о составе числа первого десятка диагностирован у 19 (83%) детей, низкий 4 (17%) детей.

При повторном проведении тестирования по методике «Что будет если..» С.Е. Гавриной в экспериментальной группе многие дети безошибочно выполнили заданий на прибавление и сложение чисел, справились с заданием на получение числа путем вычитания единицы из следующего за ним в ряду.

В контрольной группе дети вновь затруднялись при выполнении почти всех заданий на прибавление и сложение чисел, не могли без помощи воспитателя получить число путем вычитания единицы из следующего за ним в ряду.

Для сравнения показателей развития знаний о составе числа первого десятка на констатирующем и контрольном этапах исследования использовался метод t-критерия Стьюдента для зависимых выборок. В экспериментальной группе для показателей развития знаний о составе числа первого десятка было получено значение t-критерия Стьюдента равное 2,8. Полученный показатель позволил сделать вывод о существовании значимого различия показателей развития знаний о составе числа первого десятка у детей экспериментальной группы (Приложение 8, Таблица 2).

В контрольной группе полученное значение t-критерия Стьюдента равно 0,2, что позволяет говорить об отсутствии статистически значимого различия показателей развития знаний о составе числа первого десятка на констатирующем и контрольном этапах у детей в контрольной группе (Приложение 9, Таблица 2).

Повторное тестирование по методике Е.В. Колесниковой показало результаты, которые отраженны в Приложении 7 (Таблица 3). Сравнение показателей констатирующего и контрольного этапов диагностики умений считать в пределах десяти, пользоваться количественными и порядковыми числительными отражены на рисунке 2.7.

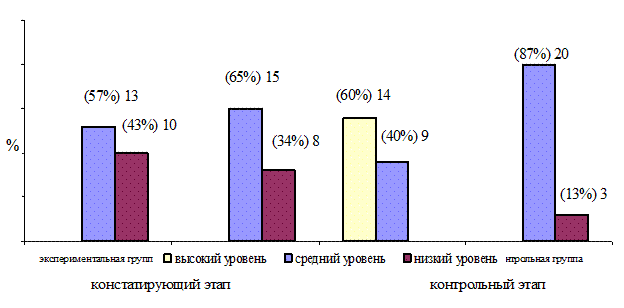
Рис. 2.7. Сравнение результатов диагностики по методике «Скажи, сколько?» Е.В. Колесниковой на констатирующем и контрольном этапах

На рисунке 2.7. можно видеть явные отличия уровня развития умения считать в пределах десяти, пользоваться количественными и порядковыми числительными у детей экспериментальной и контрольной групп на контрольном этапе исследования.

Проведенный анализ результатов по методике «Скажи, сколько?» Е.В. Колесниковой позволил сделать следующие выводы. На констатирующем этапе в экспериментальной группе высокий уровень умения считать в пределах десяти, пользоваться количественными и порядковыми числительными не показал ни один ребенок, средний уровень 13 (57%) детей; низкий уровень 10 (43%) детей. На контрольном этапе в экспериментальной группе показатели явно улучшились: высокий уровень выявлен у 14 (60%) детей; средний уровень 9 (40%) детей; низкий уровень умения считать в пределах десяти, пользоваться количественными и порядковыми числительными обнаружен не был.

В контрольной группе показатели уровня умения считать в пределах десяти, пользоваться количественными и порядковыми числительными на констатирующем и контрольном этапах остались без изменения. На констатирующем этапе высокий уровень умения считать в пределах десяти, пользоваться количественными и порядковыми числительными не обнаружен, средний уровень показали у 15 (65%) детей, низкий - 8 (34%) детей. На контрольном этапе средний уровень умения считать в пределах десяти, пользоваться количественными и порядковыми числительными выявлен у 20 (87%) детей, низкий 3 (13%) детей.

Проведение повторного тестирования по методике «Скажи, сколько?» Е.В. Колесниковой в экспериментальной группе показало, что многие дети безошибочно считают (отсчитывают) предметы в пределах 10, пользуются количественными числительными называя количество предметов и отвечая на вопрос «Сколько?», «Который по счету?». В контрольной группе многие дети вновь не могли верно выполнить задание на счет (отсчитывание) предметов в пределах 10, ошибались пользуясь количественными числительными, допускали ошибки отвечая на вопросы «Сколько?», «Который по счету?».

Сравнение полученных результатов тестирования на констатирующем и контрольном этапах было проведено с помощью метода t-критерия Стьюдента. В экспериментальной группе было получено значение t-критерия Стьюдента равное 2,9, что позволяет сделать вывод о существовании различия между показателями уровня развития умения считать в пределах десяти, пользоваться количественными и порядковыми числительными (Приложение 8, Таблица 3). В контрольной группе при сравнении показателей было получено значение t-критерия Стьюдента равное 0,2. На основании полученного показателя был сделан вывод об отсутствии статистически значимого различия между показателями развития умения считать в пределах десяти, пользоваться количественными и порядковыми числительными у детей контрольной группы на констатирующем и контрольном этапах (Приложение 9, Таблица 3).

Повторное проведение тестирования по методике «Какой цифры не стало?» Е.А. Носовой позволило получить результаты, показанные в Приложении 7 (Таблица 4). Сравнение показателей уровня развития представлений о числах на констатирующем и контрольном этапах представлено на рисунке 2.8.

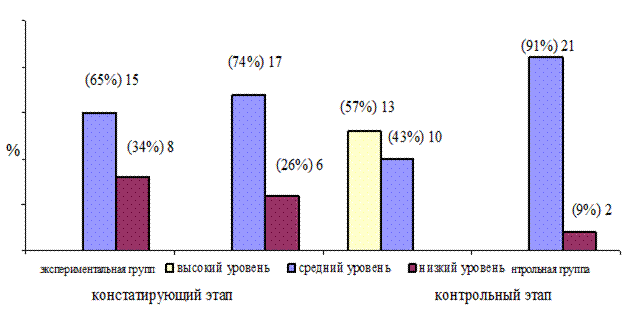
Рис. 2.8. Сравнение результатов диагностики по методике «Какой цифры не стало?» Е.А. Носовой на констатирующем и контрольном этапах

На рисунке 2.8. видно отличие уровня развития представлений о числах у детей экспериментальной и контрольной групп на контрольном этапе исследования.

В результате анализа показателей полученных по методике «Какой цифры не стало?» Е.А. Носовой были сделаны следующие выводы. На констатирующем этапе в экспериментальной группе высокий уровень развития представлений о числах не был выявлен, средний уровень был обнаружен у 15 (65%) детей; низкий уровень у 8 (34%) детей. На контрольном этапе в экспериментальной группе были получены значительно улучшенные показатели: высокий уровень диагностирован у 13 (57%) детей; средний уровень у 10 (43%) детей; низкий уровень развития представлений о числах не обнаружен.

В контрольной группе показатели развития представлений о числах на констатирующем и контрольном этапах значительно не изменились. На констатирующем этапе высокий уровень данных представлений не был обнаружен ни у одного ребенка, средний уровень показали у 17 (74%) детей, низкий - 6 (26%) детей. На контрольном этапе средний уровень развития представлений о числах выявлен у 21 (91%) детей, низкий у 2 (9%) детей.

Проведение повторного тестирования по методике «Какой цифры не стало?» Е.А. Носовой в экспериментальной группе показало, что почти все дети безошибочно определяют изменения в ряду цифр, верно называют порядок расположения цифр. В контрольной группе дети вновь ошибаются при определении изменения в ряду цифр, не могут назвать порядок расположения цифр.

Сравнение результатов тестирования на констатирующем и контрольном этапах было проведено с помощью метода t-критерия Стьюдента. В экспериментальной группе было получено значение t-критерия Стьюдента равное 2,5 что позволяет сделать вывод о существовании различия между показателями уровня развития представлений о числах (Приложение 8, Таблица 3).

В контрольной группе сравнение показателей позволило получить значение t-критерия Стьюдента равное 0,1 и дало основание сделать вывод об отсутствии статистически значимого различия между показателями развития представлений о числах у детей контрольной группы на констатирующем и контрольном этапах (Приложение 9, Таблица 4).

Таким образом, анализ результатов проведенного обследования на констатирующем и контрольном этапах с помощью диагностической беседы «Самое непохожее», тестов «Что будет, если…», «Скажи сколько?» и «Какой цифры не стало?» позволил сделать вывод о том, что в экспериментальной группе диагностируемые показатели уровня освоения логических операций, развития знаний о составе числа первого десятка, умений считать в пределах десяти, пользоваться количественными и порядковыми числительными и уровня развития представлений о числах значительно улучшились. В контрольной группе значительного изменения показателей развития логического мышления и количественных представлений выявлено не было. Достоверность различий показателей в экспериментальной группе и отсутствие статистически значимого отличия в контрольной группе доказаны с помощью t-критерия Стьюдента.

Работа, проведенная в экспериментальной группе среди детей старшего дошкольного возраста, позволила сформулировать следующие рекомендации по формированию количественных представлений средствами логического мышления:

1. Необходимо проводить предварительное планирование предстоящей работы по формированию количественных представлений на основе изучения научно-методической литературы и подбора форм, методов и средств использования логического мышления, в соответствии с возрастными особенностями детей и по результатам проведенного обследования.

2. Для эффективной работы должны быть четко сформулированы задачи в соответствии с возрастными этапами формирования количественных представлений. В старшем дошкольном возрасте это развитие представлений детей о составе числа, умений считать (отсчитывать) в пределах 10 путем, пользоваться количественным и порядковыми числительными, развитие представлений о числах, которые реализуются с использованием средств логического мышления, овладения логическими операциями анализа, синтеза, сравнения и обобщения.

3. Начальным этапом работы должно стать оформление предметно-развивающей среды в группе, в которую должны входить такие компоненты как предметное содержание (используемые материалы, игры, предметы для счета и выполнения математико-логических заданий), пространственной организации (удобное расположение в группе, достаточное освещение, возможность участия всех детей в организованных и самостоятельных формах работы), изменяемость содержания в зависимости от темы и времени использования.

4. Содержание предметно-развивающей среды в группе необходимо наполнить доступными и разнообразными средствами помогающими сформировать количественные представления детей в организованной и самостоятельной деятельности. Необходимо чтобы это были интересные, яркие и современные математико-логические игры, предметы и игровые материалы, конструкторы, пазлы, наборы для счета. Возможно пополнение предметно-развивающей среды в группе любимыми играми самих детей, принесенными для своих друзей в группе, изготовленных вместе с родителями.

5. В работе по формированию количественных представлений математические средствами логического мышления необходимо использовать современные учебно-методические пособия, логические модели, которые помогут детям овладеть логическими операциями и сформировать количественные представления в процессе нагляно-практической деятельности. К таким пособиям относятся счетная и числовая лесенки, обучающие книги и картинки для раскрашивания, счетное лото, которые также способствуют развитию интереса к получению математических знаний, приучают детей к самостоятельной счетной деятельности.

6. Для закрепления количественных представлений необходимо также использовать материалы и оборудование для разных видов самостоятельной вычислительной деятельности детей: счета в пределах 10, развития знаний о составе числа, представлений о числах. Использование счетных игр, оборудования для измерений количества мелких предметов, позволит использовать и закрепить логические операции сравнения, обобщения, анализа и синтеза.

7. Рекомендуется регулярно обновлять материалы и оборудование находящиеся в предметно-развивающей среде, обеспечить их доступность для самостоятельных игр детей, индивидуальных упражнений, выбор по интересам детей и в соответствии с проводимой в данное время работой в образовательной деятельности. Например, если в организованной образовательной деятельности формируется представление о числах, то дети должны иметь возможность самостоятельно раскрашивать, лепить группы предметов по заданному воспитателем числу, играть в настольные и печатные игры в которых есть возможность отгадывать номер того или иного предмета по порядку, в обратном порядке.

8. Для формирования количественных представлений рекомендуется использовать разные виды деятельности детей, способствующие развитию операций логического мышления: организованную образовательную деятельность, совместную предметную деятельность воспитателя с детьми, самостоятельные логико-математические игры детей, самостоятельную вычислительную деятельность детей, совместные математические игры воспитателя с детьми, словесные игры воспитателя с детьми, математические развлечения, работа по загадкам и чтение.

9. В основе формирования количественных представлений должна быть работа по развитию представлений о количественных отношениях, о числе, числовом ряде. Эта работа должна быть построена на основе использования средств наглядности. Для этого в организованной образовательной деятельности, играх, упражнениях и заданиях можно использовать логические числовые модели, позволяющих одновременно закрепить умение сравнивать, синтезировать и обобщать, развивать представления о составе чисел из единиц. Такие модели могут быть изготовлены родителями детей, разукрашены самими детьми. Это позволит заинтересовать их, сделать нелегкий процесс освоения количественных представлений более эмоциональным, увлекательным и радостным.

10. Формирование знаний о составе числа первого десятка рекомендуется использовать наглядный прием показа состава числа из единиц на конкретном математико-логическом материале. Для этого необходимо использовать игры, упражнения и задания на разные логические операции: составление групп из разных предметов по признакам; счет предметов и групп предметов, объединенных одним признаком; составление группы предметов по количественным и качественными признакам; составление группы из картинок, объединенных родовым понятием.

11. Необходимо так организовать работу, чтобы дети могли осуществлять отсчитывание, пересчитывание, называние числа предметов, в конкретной предметной деятельности. Это могут быть рисование, лепка, закрашивание, которые дадут возможность закрепить умение использовать логические операции в организованной и самостоятельной деятельности, а также в повседневной жизни в детском саду.

12. Для развитие понимания детьми количественного состава чисел рекомендуется вести работу одновременно с несколькими числами, использовать с этой целью упражнения на составление групп по заданному количеству предметов. при этом важно, чтобы используемый материал был разнообразным, ярким, интересным для детей, чтобы каждый ребенок мог рассказать о том, что они делают, какое задание выполняют, что у них получается, рассказать о группах предметов их сходствах и отличиях.

13. Порядковый счет в пределах 10, умение пользоваться количественными и порядковыми числительными необходимо формировать используя такой развивающий прием как проблемные вопросы. Эти вопросы способствуют усвоению детьми назначения количественного и порядкового счета. В повседневной жизни детей в детском саду, в образовательной деятельности, играх и предметной деятельности нужно приводить примеры использования порядковых числительных (номера домов, квартир, маршрутных автобусов), способствовать проявлению жизненного опыта детей связанного с использование количественного и порядкового счета, давать возможность детям рассказать о том, где они могли видеть нумерацию, наблюдать применение количественного счета (в магазине, дома, в кафе, на улице).

14. После усвоения детьми навыков счета и использования количественными и порядковыми числительными в работе с детьми необходимо использовать проблемные вопросы, ответы на которые предполагают использовать логических операций сравнения, анализа, обобщения, синтеза. Это можно делать как в организованной образовательной деятельности, словесных упражнениях на определение номера указанного предмета или предмета по указанному номеру, драматизациях сказок так и в повседневной жизни в детском саду.

15. Работа по формированию количественных представлений у детей экспериментальной группы средствами логического мышления должна проводиться в тесном контакте с родителями. Необходимо использовать разные формы работы, помогающие познакомить родителей с проводимой воспитателями работой, содержанием логических игр развивающих количественные представления старших дошкольников.

16. Особое место в работе с родителями старших дошкольников при формировании количественных представлений средствами логического мышления должны занимать индивидуальные беседы и рекомендации на основе индивидуального похода к каждому ребенку. Это будет способствовать не только приобщению родителей к работе, но и установлению индивидуальной обратной связи с родителями, чьи дети слабо осваивают сложные количественные представления, затрудняются в владении логическими операциями.

17. Рекомендуется проведение родительских собраний с показом организованной образовательной деятельности. Такие собрания помогут заинтересовать родителей процессом формирования количественных представлений у детей, выявить возможные трудности их усвоения, а также помогут наглядно показать родителям как проводить математико-логические игры, упражнения, как выполнять задания на овладение логическими операциями, развивать знания детей о числах, учить их считать, развивать умение использовать в речи числительные.

Таким образом, рекомендации по формированию количественных представлений у детей старшего дошкольного возраста средствами логического мышления касаются предварительного планирования работы на основе научно-методической литературы и выбора форм и методом работы соответствующих возрастным особенностям детей, формулировки задач проводимой работы, организации предметно-развивающей среды в группе (включение в нее средств формирования количественных представлений в организованной и самостоятельной деятельности средствами логического мышления), использования специально подобранных математико-логических материалов, оборудования и их регулярного обновления в зависимости от формируемых количественных представлений и тематики работы, методического содержании использования разных видов деятельности для формирования количественных представлений с использованием средств овладения логическими операциями, развития представлений о составе числа, умения считать в пределах 10, пользоваться количественными и порядковыми числительными, представлений о числах средствами логического мышления. Рекомендации также касаются взаимодействия с родителями детей в процессе проведения формирующей работы

Выводы по II главе

С целью подтверждения гипотезы исследования была проведена диагностика уровня овладения логическими операциями, уровня развития умения считать в пределах 10, пользоваться количественными и порядковыми числительными, представлений о числах, статистическое сравнение данных на констатирующем и контрольном этапах в экспериментальной и контрольной группах. Полученные результаты были проанализированы и интерпретированы.

На констатирующем этапе исследования в экспериментальной и контрольной группах были получены показатели среднего и низкого уровня овладения логическими операциями, уровня развития умения считать в пределах 10, пользоваться количественными и порядковыми числительными, представлений о числах. Было обнаружено отсутствие статистически значимого отличия полученных показателей развития логического мышления количественных представлений в исследуемых группах. Опираясь на результаты констатирующего исследования, была проведена работа по формированию количественных представлений средствами логического мышления у старших дошкольников экспериментальной группы. Задачей проведения работы с детьми в экспериментальной группе было развитие уровня овладения логическими операциями, счетных умений, пополнение речи количественными и порядковыми числительными, развитие представлений о числах на основе средств математического развития с использованием логического мышления старших дошкольников.

Формами работы с детьми были выбраны организованная образовательная деятельность, досуг, в которых использовались различные виды игр, дидактические задания и упражнения, образовательная деятельность при проведении режимных моментов, самостоятельная деятельность детей. Работа проводилась при непосредственном участии родителей детей.

Контрольное исследование по методикам констатирующего этапа, показало повышение уровня овладения логическими операциями, уровня развития умения считать в пределах 10, пользоваться количественными и порядковыми числительными, представлений о числах в экспериментальной группе. Было доказано статистически значимое отличие показателей констатирующего и контрольного этапов исследования в экспериментальной группе. В контрольной группе уровень развития логического мышления и количественных представлений изменился не значительно. С помощью математико-статистической обработки было доказано отсутствие статистически значимого различия показателей в контрольной группе на констатирующем и контрольном этапах.

Анализ и сравнение данных констатирующего и контрольного этапов исследования был сделан вывод об эффективности работы по формированию количественных представлений средствами логического мышления у старших дошкольников экспериментальной группы. Это дает основание утверждать, что ранее заявленная гипотеза подтвердилась.

Полученные результаты исследования позволили сделать рекомендации по организации форм работы, выбора средств и материалов, позволяющих эффективно использовать средства логического мышления для формирования количественных представлений у детей старшего дошкольного возраста.

Заключение общий вывод по 1 и 2 главам

С целью использования средств логического мышления в формировании количественных представлений детей старшего дошкольного возраста была проведена исследовательская работа, включающая несколько этапов. Первый этап включал анализ научно-методической литературы по проблеме развития логического мышления и формирования количественных представлений у детей в старшем дошкольном возрасте который позволил сделать следующие выводы:

1. Мышление является формой познания, воспроизведения и психического отражения действительности человеком, с целью решения задач установления связи и отношений между объектами окружающего мира. В дошкольном возрасте мышление развивается от наглядно-действенного, наглядно-образному к словесному мышлению.

2. Логическое мышление являясь высшей стадией развития мышления старших дошкольников, формируется при условии высокой активной умственной деятельности, в процессе усвоения знаний о существенных признаках предметов и явлений действительности, закрепленных в речи детей. Оно необходимо для развития умственных действий и интеллектуального развития и включает в себя следующие операции: сравнение, анализ, синтез, упорядоченность действий, классификация.

3. Развитие количественных представлений в старшем дошкольном проходит этапы от сравнения множеств к воспроизведению величин при условии овладения детьми такими видами деятельности как счет, измерение, простейшие вычисления на основе развития числовых представлений, количественного и порядкового счета, навыков использования цифр, которые применяются детьми в играх и закрепления в речи умения использовать касающиеся количества и количественных отношениях множеств предметов.

5. Методика и организация формирования числовых представлений у старших дошкольников включает в себя развитие счетной, измерительной деятельности, совершенствование умений сравнивать числа, понимать относительность числа, отношения части и целого, навыков увеличения и уменьшения чисел, подготовку к усвоению арифметических действий сложения и вычитания, на основе уже имеющихся знаний детей с использованием наглядности, словесных, игровых методов.

6. К средствам формирования количественных представлений детей старшего дошкольного возраста относятся дидактический материал, оборудование для игр и образовательной деятельности, печатные издания с наглядным материалом для самостоятельных и организованных игр и упражнений в вычислительной деятельности, разные виды математического материала. Работа по формированию количественных представлений проводится с помощью организованной и самостоятельной образовательной деятельности с детьми, игр и упражнений.

Нами была выдвинута гипотеза о том, что использование средств развития логического мышления будет способствовать у детей старшего дошкольного возраста формированию количественных представлений старших дошкольников, если:

- определить средства развития логического мышления старших дошкольников по ФЭМП соответствующие их возрастным особенностям;

- использовать средства развития логического мышления по ФЭМП для формирования количественных представлений старших дошкольников;

- разработать рекомендации по использованию средств развития логического мышления для формирования количественных представлений в дошкольной образовательной организации.

Экспериментальное исследование было организовано на базе Муниципального дошкольного образовательного учреждения «Центр развития ребенка - детский сад № 36 «Волшебный дворец» г. Альметьевск» среди детей младшего дошкольного возраста в количестве 46 человек.

Исследование проводилось в несколько этапов: констатирующий, формирующий и контрольный.

Для проведения диагностики были выбраны следующие методики: диагностическая беседа «Самое непохожее» для обследования уровня овладения детьми старшего дошкольного возраста логическими операциями; тест «Что будет если…» для определения уровня развития знаний о составе числа первого десятка; тест «Скажи, сколько?» для диагностики умения считать (отсчитывать) в пределах 10, пользоваться количественными и порядковыми числительными; тест «Какой цифры не стало?» для выявления развития представлений о числах у детей старшего дошкольного возраста.

Диагностика уровня овладения логическими операциями по методике «Самое непохожее» Л.А. Венгера показала, что в двух группах слабо развиты умения определять различия и сходства геометрических фигур, находить отличающуюся от остальных геометрическую фигуру, называть все ее существенные отличия. Обследование уровня развития знаний о составе числа первого десятка с помощью «Что будет, если…» С.Е. Гавриной позволило установить у детей в обеих группах затруднения при выполнении почти всех заданий на прибавление и сложение чисел, получение числа путем вычитания единицы из следующего за ним в ряду. Проведение методики «Скажи, сколько?» Е.В. Колесниковой в обеих группах многие дети показали слабо развитые умения считать в пределах 10, пользовались количественными числительными. Проведение тестирования по методике «Какой цифры не стало?» В.П. Новиковой показало, что в обеих группах слабо развито представление о числах.

Математико-статистическая обработка результатов обследования по всем методикам с помощью t-критерия Стьюдента показала отсутствие достоверного различия показателей уровня развития логического мышления и количественных представлений в экспериментальной и контрольной группах на констатирующем этапе.

На формирующем этапе на основе результатов обследования был составлен перспективный план по формированию количественных представлений старших дошкольников экспериментальной группы средствами логического мышления. С учетом возрастных особенностей детей были проведены разнообразные формы учебно-воспитательной работы, направленные на овладение логическими операциями, развитие знаний о составе числа, умений считать в пределах десяти и использовать количественные и порядковые числительные, повышение уровня представлений о цифрах. Формами работы были выбраны образовательная деятельность, самостоятельная деятельность детей, досуги, организация предметно-пространственной среды, в которых использовались средства логического мышления для формирования количественных представлений детей. На протяжении всей формирующей работы было организовано сотрудничество с родителями воспитанников.

На контрольном этапе с помощью методик констатирующего этапа, было проведено повторное обследование уровня овладения логическими операциями, развития знаний о составе числа первого десятка, умений считать в пределах 10 и пользоваться количественными и порядковыми числительными, а также уровня развития представлений о числах в экспериментальной и контрольной группах. Повторное обследование позволило установить, что в экспериментальной группе показатели развития логического мышления и сформированности количественных представлений значительно изменились, в контрольной группе данные по всем методикам остались без значительных изменений. Анализ и сравнение результатов исследования по всем методикам показал значительное повышение уровня развития логического мышления и количественных представлений в экспериментальной группе, в контрольной группе значительной динамики показателей развития логического мышления и количественных представлений не выявлено.

Статистическая обработка данных до формирующего эксперимента и после с помощью метода t-критерия Стьюдента позволило выявить значимость отличия в показателях экспериментальной группе и их отсутствие в контрольной группе.

На основании полученных результатов исследования был разработан комплекс рекомендаций по организации планирования, определения задач проводимой работы, оснащения предметно-развивающей среды в группе, выбора и использования материалов и оборудования, методики развития количественных представлений детей средствами логического мышления.

Таким образом, сравнение результатов контрольного исследования с данными констатирующего исследования показало эффективность проведенной работы по формированию количественных представлений детей старшего дошкольного возраста средствами логического мышления. Следовательно, заявленная гипотеза исследования подтвердилась.

Список использованной литературы

1. Альтхауз, Д.С. Цвет, форма, количество / Д.С. Альтхауз. - М.: Педагогика, 2010. – 98 с.

2. Анищенко, О.М. Возможность формирования логического мышления в детстве / О.М. Анищенко. – М.: Класс, 2009. – 89 с.

3. Блехер, Ф.Н. Счет и число в детском саду / Ф.Н. Блехер. - М.: Класс, 2011. – 120 с.

4. Блонский, П.П. Память и мышление дошкольников / П.П. Блонский. - М.: Психология и педагогика, 2008. - 269 с.

5. Венгер, В.А. Развитие познавательных способностей в процессе дошкольного воспитания / В.А. Венгер. - М.: АСТ, 2010. – 258 с.

6. Водопьянов, Е.Н. Формирование начальных математических понятий у дошкольников / Е.Н. Водопьянов // Дошкольное воспитание. - М., 2007. - № 3. - С. 36-37.

7. Выготский, Л.С. Мышление и речь. Проблемы психологического развития ребенка / Л.С. Выготский. - М.: Апрель, 2010. – 520 с.

8. Гаврина, С.Е. Учусь считать / С.Е. Гаврина. - М.: ДиК, 2011. – 102 с.

9. Грин, Р.М. Введение дошкольника в мир числа / Р.М. Грин. - М.: Класс, 2010. – 75 с.

10. Гурова, Л.Л. Развитие детского мышления / Л.Л. Гурова. – М.: Библион, 2008. – 230 с.

11. Данилова, А.В. Обучение математике в детском саду / А.В. Данилова. - М.: Академия, 2007. – 65 с.

12. Ендовицкая, Т.В. Развитие мышления в дошкольном возрасте / Т.В. Ендовицкая. - М.: Проспект-М, 2010. – 145 с.

13. Житомирский, В.Г. Математическая азбука / В.Г. Житомирский. - М.: Проспект-М, 2010. – 178 с.

14. Зайцев, В.В. Математика для детей дошкольного возраста / В.В. Зайцев. - М.: Диалог, 2009. – 78 с.

15. Запорожец, А.В. Условия и движущие причины психического развития / А.В. Запорожец. - М.: Ацрис-Пресс, 2009. - 267 с.

16. Калинченко, А.В. Обучение математике детей дошкольного возраста / А.В. Калинченко. - М.: Айрис-пресс, 2010. – 118 с.

17. Касицина, М.А. Дошкольная математика / М.А. Касицина. - М.: ГНОМ и Д, 2009. – 112 с.

18. Колесникова, Е.В. Развитие основ математического мышления в детском саду / Е.В. Колесникова. - М.: Гном-Пресс, 2013. – 114 с.

19. Корнеева, Г.А. Современные подходы к обучению детей дошкольного возраста математике / Г.А. Корнеева // Дошкольное воспитание. - М., 2010. - № 2. - С. 6-7.

20. Корнеева, Г.А. Теория и методика развития математического представления у дошкольников / Г.А. Корнеева. - М.: Бином, 2011. – 85 с.

21. Костюк, Г.С. Избранные психологические труды / Г.С. Костюк. - М.: Аванта-Пресс, 2011. – 185 с.

22. Левина, М.З. Логика и математика для дошкольников в детском саду / М.З. Левина. - СПб.: Акцидент, 2013. - 79 с.

23. Леонтьев, А.Н. Избранные психологические произведения / А.Н. Леонтьев. – М.: Класс, 2010. – 189 с.

24. Леушина, А. М. Формирование элементарных математических представлений у дошкольников / А.М. Леушина. - М.: Класс, 2008. – 115 с.

25. Леушина, А.М. Занятия по счету в детском саду / А.М. Леушина. - М.: ДиК, 2009. – 185 с.

26. Менчинская, Н.А. Психология обучения детей дошкольного возраста арифметике / Н.А Менчинская. - М.: Наука, 2012. – 196 с.

27. Метлина, Л.С. Математика в детском саду / Л.С. Метлина. - М.: АРКТИ, 2012. – 228 с.

28. Михайлова, 3.А. Игровые задачи для развития логического мышления дошкольников / З.А. Михайлова. - СПб.: Питер, 2011. – 81 с.

29. Михайлова, З.А. Теории и технологии математического развития дошкольников. / З.А. Михайлова. - СПб: Питер, 2010. – 85 с.

30. Непомнящая, Н.И. Логика и математика для дошкольников / Н.И. Непомнящая. - М.: Прогресс, 2010. – 115 с.

31. Носова, Е.А. Совершенствование процесса формирования элементарных математических представлений в детском саду / Е.А. Носова. - СПб.: Питер, 2013. – 178 с.

32. Петерсон, Л.Г. Практический курс математики для дошкольников. Методические рекомендации / Л.Г. Петерсон. – М.: Класс, 2013. – 176 с.

33. Пиаже, Ж. Избранные психологические труды / Ж. Пиаже. – М.: АГРАФ, 2010. – с. 389.

34. Плаксина, Л.И. Математика в детском саду / Л.И. Плаксина. - М.: Мозаика-Синтез, 2012. – 136 с.

35. Поддъяков, Н.Н. Развитие мышления и умственное воспитание дошкольника / И.Н. Поддъяков. - М.: Проспект-М., 2013. – 189 с.

36. Сербина, Е.В. Математика для малышей / Е.В. Сербина. - М.: Наука, 2009. – 241 с.

37. Соловьева, Е.В. Математика и логика для дошкольников / Е.В. Соловьева. - М.: Астрель, 2010. – 85 с.

38. Соловьева, Е.В. Математика и логика для дошкольников / Е.В. Соловьева. - М.: Академия, 2010. - 216 с.

39. Столяр, А.А. Формирование элементарных математических представлений у дошкольников / Столяр А.А. – М.: Класс, 2008. – 163 с.

40. Тарунтаева, Т.В. Развитие элементарных математических представлений / Т.В. Тарунтаева. - М.: Астрель. - 197 с.

41. Тарханова, Е. А. Формирование у детей знаний арифметических действий / Е.А. Тарханова – М.: Академия, 2012. – 256 с.

42. Тихеева, Е.И. Счет в жизни маленьких детей / Е.И. Тихеева. – М.: Проспект, 2009. – 120 с.

43. Ушинский, К. Д. О первоначальном обучении счету / К.Д. Ушинский. – М.: Феникс, 2008. – 75 с.

44. Фалькович, Т.А. Формирование математических представлений. - / Т.А. Фалькович. – М.: ВАКО, 2011. - 208 с.

45. Федлер, М. Математика уже в детском саду / М. Федлер. - М.: Эксмо, 2010. – 118 с.

46. Филиппова, Е.В. Предпосылки формирования логических операций у детей дошкольного возраста / Е.В. Филиппова. - М.: АРКТИ, 2008. – 102 с.

47. Фрейлах, Н.И. Методика математического развития / Н.И. Фрейлах- М.: ФОРУМ, 2011. - 236 с.

48. Фридман, Л.М. Психолого-педагогические основы обучения математики / Л.М. Фридман. – М.: Наука, 2011. – 156 с.

49. Фунтикова, О.А. Теоретические основы математического развития дошкольников / О.А. Фунтикова. - М.: Мозаика - Ситнтез, 2011. – 185 с.

50. Шмаков, С.А. Умственная деятельность и развитие / С.А. Шмаков // Вопросы психологии. – 2009, №5. - С. 43-48.

51. Щербакова, Е.И. Теория и методика математического развития дошкольников / Е.И. Щерббакова. - Воронеж, 2009. - 228 с.

52. Эльконин, Д.Б. Воспитание интеллекта / Д.Б. Эльконин. - М.: ИТРК, 2009. – 297 с.

53. Якиманская, И.С. Умственное развитие в период детства / И. С. Якиманская. – М.: ДиК, 2010. – 85 с.

54. Ярошенко, М.Г. Основы умственного воспитания в детском саду / М.Г. Ярошенко. – М.: Класс, 2011. – 75 с.

Приложение 1

Образец материала и содержание «ключа» для оценки заданий к методике «Самое непохожее» Л.А. Венгера

Материалом служат 8 плоских геометрических фигурок, различающихся по форме, цвету, величине: 4 квадрата, 4 круга. Четыре фигуры одного цвета (один круг маленький, другой – большой; один квадрат – маленький, другой – большой). Остальные фигуры – другого цвета:

Задание № 1 (на развитие логической операции анализа): воспитатель раскладывает фигурки в ряд и в произвольной последовательности и говорит ребенку: «Посмотри, какие здесь фигурки. Посмотри и скажи, чем они отличаются друг от друга».

Задание № 2 (на развитие логической операции синтеза): после выполнение задания № 1 взрослый подводит итог: «Значит, здесь есть фигурки квадратные и круглые, красные и синие, большие и маленькие». Указывая на две фигурки, различающиеся по одному из параметров (например, большой и маленький синие квадраты), спрашивает: «Чем эти фигурки отличаются друг от друга?».

Задание № 3 (на развитие операции сравнения): воспитатель раскладывает 3 фигуры в ряд, среди которых две одинаковые по форме, но одинаковые по цвету и одна отличается от них по форме и просит: «Найди среди фигурок самую не похожую на эти. Самая непохожая – только одна».

Задание № 4 (на развитие логической операции обобщения): выбранную в предыдущем задании фигурку кладут рядом с другой фигуркой - образцом и спрашивают: «Почему ты считаешь, что эти фигурки самые непохожие?». Каждый ребенок выполняет задание с 2-3 разными фигурками.

«Ключ» для оценки выполнения заданий:

Задание № 1:

3 балла - названы все различия (цвет, форма и величина; синие и красные; большие и маленькие; круги и квадраты);

2 балла – названы не все различия (либо цвет и форма, либо форма и величина, либо цвет и величина; после помощи воспитателя названы отличия в размере);

1 балл – названы 1-2 различия, помощь воспитателя не облегчает выполнение задания.

Задание № 2:

3 балла – ребенок верно выделяет признаки сходства двух одинаковых геометрических фигур (количество сторон, углов, цвет);

2 балла – названы не все признаки; после помощи воспитателя названы остальные признаки;

1 балл – назван 1 признак, с трудом называется еще 1 признак сходства.

Задание № 3:

3 балла – ребенок верно нашел отличающуюся фигуру;

2 балла – ребенок с трудом нашел отличающуюся фигуру;

1 балл – ребенок нашел отличающуюся фигуру после предложенной помощи воспитателя.

Задание № 4:

3 балла – ребенок называет существенные различия при сравнении двух фигур (цвет, форму и величину, количество углов и сторон);

2 балла – называет не все существенные различия двух фигурок, не указывая отличия в количестве углов и сторон;

1 балл – названы 1-2 различия.

«Ключ» для оценки результатов тестирования:

высокий уровень - 12 - 11 баллов - ребенок владеет логическими операциями: выделяет все различия геометрических фигур, признаки их сходства, находит отличающуюся фигуру, называет существенные развития двух разных фигур;

средний уровень - 10 - 8 баллов ребенок не в полной мере овладел логическими операциями: выделяет часть различий геометрических фигур, называет не все признаки их сходства, находит отличающуюся фигуру, называет не все существенные различия двух разных фигур;

средний уровень – 7 и менее баллов ребенок не владеет логическими операциями: не умеет выделять все различия геометрических фигур и признаки их сходства, с трудом находит отличающуюся фигуру, не может самостоятельно назвать существенные различия двух разных фигур.

Приложение 2

Содержание методики «Что будет если…» С.Е. Гавриной

Диагностические вопросы для детей:

Подумай и дай правильный ответ:

- Что будет, если к 7 прибавить 1? (Получится число 8);

- Что будет, если к 9 прибавить 1;

- Как получить число 8, если есть число 9? (Убрать одну единицу);

- Что будет если сложить три единицы? (Получится число 3);

- А если сложить 5 единиц? (Число 5).

«Ключ»:

3 балла - ребенок знает состав чисел первого десятка (из отдельных единиц) и как получить каждое число первого десятка, прибавляя единицу к предыдущему и вычитая единицу из следующего за ним в ряду.

2 балла - ребенок знает состав чисел первого десятка (из отдельных единиц), затрудняется при выполнении заданий, касающихся знаний о получении числа путем вычитания единицы из следующего за ним в ряду.

1 балл - ребенок допускает большое количество ошибок при выполнении заданий.

Приложение 3

Содержание методики «Скажи сколько» Е.В. Колесниковой

Материал: предметные картинки или мелкий счетный материал: матрешки, солдатики, овощи, цветы и т.п. Количество каждой группы предметов разное (например, 6 матрешек, 7 цветов, 9 солдатиков, 10 бабочек).

Вопросы ребенку:

- Посчитай солдатиков. Сколько их всего?

- Посчитай бабочек. Сколько их? И т. д.

«Ключ»:

3 балла - ребенок правильно считает (отсчитывает) предметы в пределах 10. Правильно пользуется количественными и порядковыми числительными. Понимает и правильно отвечает на вопросы «Сколько?», «Который по счету?».

2 балла - ребенок правильно считает (отсчитывает) предметы в пределах 10, но неуверенно пользуется количественными числительными. Понимает вопрос «Сколько?», но неуверенно отвечает на него. Допускает ошибки при ответе на вопрос «Который по счету?».

1 балл - ребенок допускает ошибки при счете (отсчитывании) предметов.

Приложение 4

Содержание методики «Какой цифры не стало?» Е.А. Носовой

Ход проведения обследования: Перед ребенком раскладываются цифры, затем ребенка просят закрыть глаза и убирают одну-две цифры. Ребенок должен не только заметить изменения, но и сказать, где какая цифра стоит и почему. Например, цифра 5 сейчас стоит между 7 и 8 (или она исчезла). Ее место между цифрами 4 и 6, потому что число 5 больше 4 на один, 5 должна стоять после 4.

За каждый правильный ответ дети получают 1 балл.

«Ключ»:

5 баллов - ребенок верно замечает изменения в ряду цифр, верно называет порядок расположения цифр.

4-3 балла - ребенок допускает незначительные ошибки при определении изменения в ряду цифр, но верно называет порядок расположения цифр.

2 балла - ребенок не справляется с заданием.

Приложение 5