Абсолютные и относительные показатели.
Каждый ряд распределения характеризуется рассеиванием индивидуальных значений признака, т.е. значительным или незначительным несовпадением уровней своих значений. Для измерения рассеяния (вариации) признака применяются абсолютные и относительные показатели вариации.
Кабсолютным показателям вариацииотносится размах вариации – это разность между максимальным и минимальным значениями признака в совокупности:
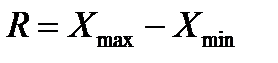 . (3.1)
. (3.1)
Размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов значений признака.
Для измерения среднего по совокупности отклонения значения признака от его среднего уровня используют среднее квадратическое (стандартное)отклонение или его квадрат, являющийся дисперсией
или его квадрат, являющийся дисперсией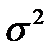 .Их выборочные оценки будем обозначать
.Их выборочные оценки будем обозначать 
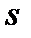 и
и 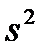 .
.
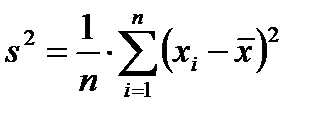 , (3.2)
, (3.2)
Дисперсия (и как корень квадратный – среднее квадратическое отклонение) может вычисляться с помощью более простой формулы:
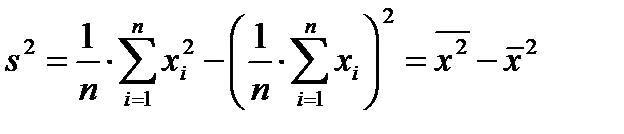 . (3.3)
. (3.3)
Для сравнения изменчивости различных признаков вычисляется относительный показатель – коэффициент вариации
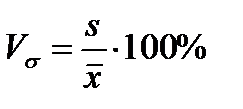 . (3.4)
. (3.4)
Коэффициент вариации является характеристикой однородности совокупности. Так совокупность считается качественно однородной, если коэффициент вариации не превышает 33 %.
| Пример 3.1.Имеются данные измерений роста шести человек
Определить показатели вариации.
|
3.2. Виды дисперсий и правило сложения дисперсий.
Для определения степени зависимости вариации признака от некоторого фактора, всю статистическую совокупность делят на группы по числу уровней этого фактора. Влияние фактора можно оценить сравнивая межгрупповую (факторную) и внутригрупповую (остаточную) вариации признака. Соответственно рассматривают дисперсии: общую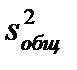 , факторную
, факторную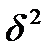 и остаточную
и остаточную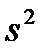 .
.
Справедливо следующее статистическое тождество (правило сложения дисперсий):
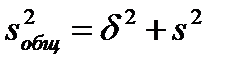 . (3.5)
. (3.5)
Пусть исходная совокупность делится на 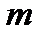 однородных групп по одному фактору (т.е. фактор с
однородных групп по одному фактору (т.е. фактор с 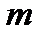 уровнями), в каждой по
уровнями), в каждой по 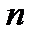 элементов:
элементов:
Номер испытания, 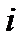
| Уровни фактора, 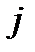
| |||
| ... | 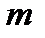
| |||
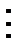
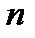
| 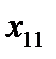
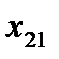
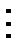
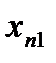
| 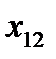
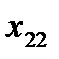
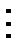
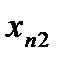
| …
…
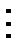 ...
...
| 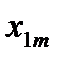
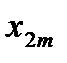
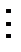
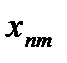
|
| Групповые средние | 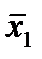
| 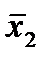
| … | 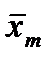
|
Сначала находятся 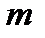 частных средних в каждой группе:
частных средних в каждой группе:
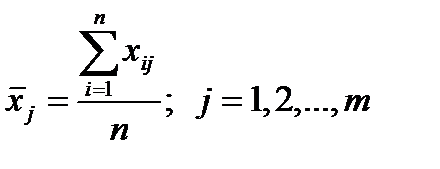 . (3.6)
. (3.6)
Далее, определяется общая средняя как средняя арифметическая этих частных средних:
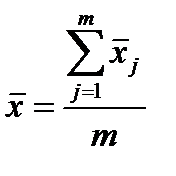 . (3.7)
. (3.7)
Тогда общая дисперсия, отражающая вариацию признака за счет всех факторов, действующих в данной совокупности, рассчитывается по формуле
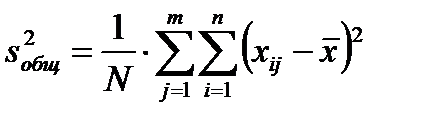 , (3.8)
, (3.8)
где 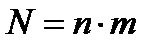 – число наблюдений .
– число наблюдений .
Факторная дисперсия характеризует вариацию за счет признака-фактора, положенного в основу группировки, и равна:
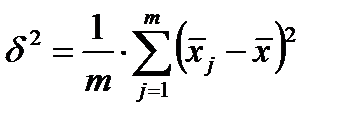 . (3.9)
. (3.9)
Остаточная дисперсия характеризует вариацию признака, не связанную с делением совокупности на группы, и вычисляется по формуле:
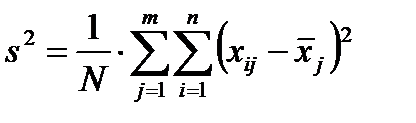 . (3.10)
. (3.10)
Соотношение факторной и общей дисперсии называется коэффициентом детерминации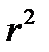 и показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки:
и показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки:
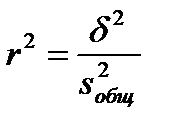 . (3.11)
. (3.11)
Для проверки гипотезы о влиянии фактора используется критерий Фишера:
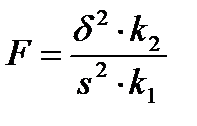 , (3.12)
, (3.12)
где 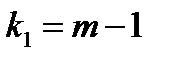 и
и 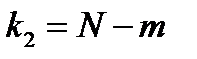 − число степеней свободы для сравниваемых дисперсий.
− число степеней свободы для сравниваемых дисперсий.
Чем больше влияние факторного (группировочного) признака на результативный, тем больше значение 
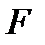 .
.
Расчетное значение 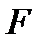 сравнивается с критическим
сравнивается с критическим 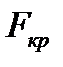 , определяемым по таблице в зависимости от числа степеней свободы и уровня значимости
, определяемым по таблице в зависимости от числа степеней свободы и уровня значимости 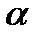 . Если
. Если 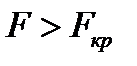 , то факторный признак оказывает влияние на исследуемый признак. Если
, то факторный признак оказывает влияние на исследуемый признак. Если 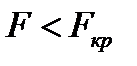 , то только с вероятностью не выше чем
, то только с вероятностью не выше чем 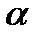 случайные значения величины
случайные значения величины 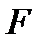 будут превышать расчетное значение. Следовательно, с малой вероятностью
будут превышать расчетное значение. Следовательно, с малой вероятностью 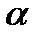 факторный признак будет оказывать влияние на результативный признак и это влияние можно не учитывать.
факторный признак будет оказывать влияние на результативный признак и это влияние можно не учитывать.
Пример 3.2. Банк имеет по четыре отделения в трех городах. Текущие объемы денежных вкладов (в условных единицах) представлены в таблице:
Можно ли утверждать на уровне значимости Вычисляем групповые средние Межгрупповая (факторная) дисперсия (3.9):
Групповая (остаточная) дисперсия (3.10):
Вариация, обусловленная влиянием всех факторов, вместе взятых, определится общей дисперсией (3.5):
Полученный коэффициент детерминации (3.11):
показывает, что дисперсия зависит от места расположения отделений на 52,3%; остальные же 47,7 % объясняются множеством других неучтенных факторов. Для проверки гипотезы о влиянии фактора используем критерий Фишера (3.12):
Для |
Дата добавления: 2016-06-02; просмотров: 1317;

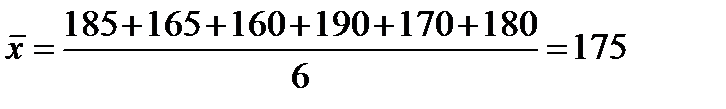 ;
;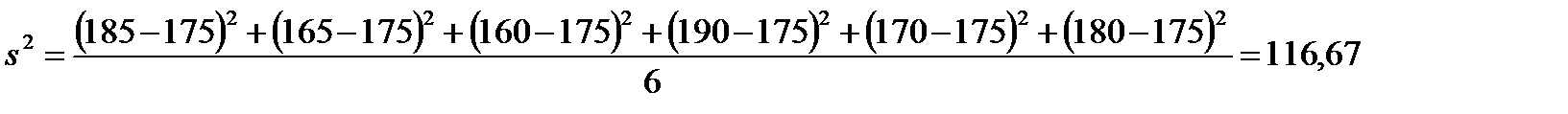 ;
;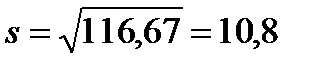 ;
; 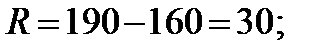
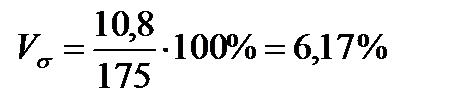 .
.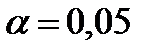 , что в среднем дела идут одинаково хорошо во всех трех городах?
, что в среднем дела идут одинаково хорошо во всех трех городах?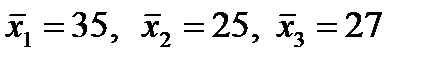 и общее среднее
и общее среднее 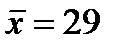 .
.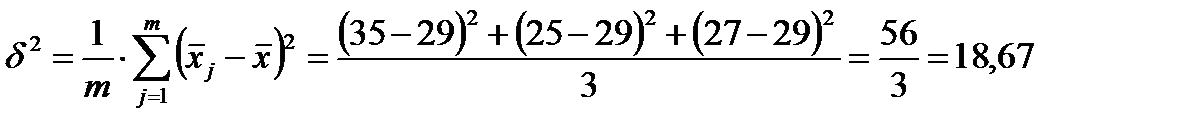 ;
;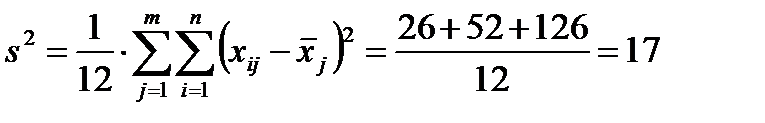
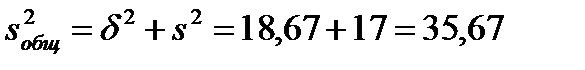 .
.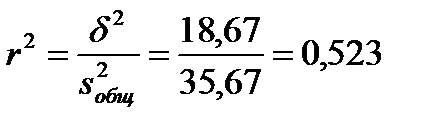
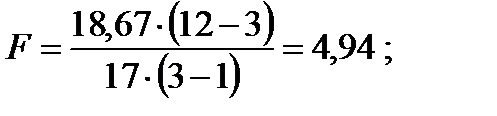
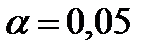
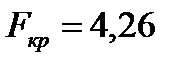 . Следовательно,
. Следовательно,