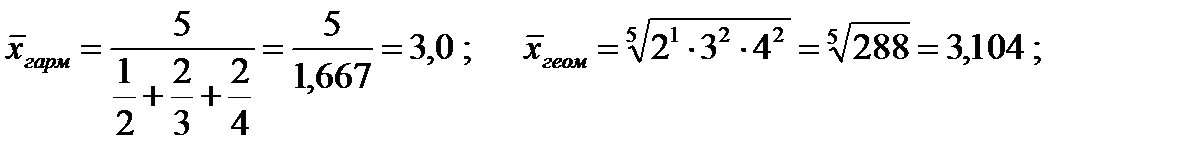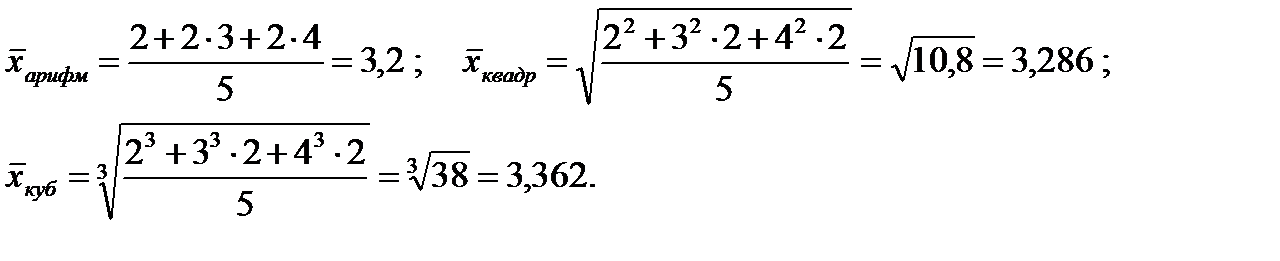Структурные средние.
Мода (Мо)–это наиболее часто встречающееся (т.е. с наибольшей частотой), значение признака у элементов совокупности. Если признак дискретная величина, мода равна значению, которое повторяется наиболее часто. Например, в группе из 11 студентов получены следующие баллы за тест: 5, 4, 3, 7, 9, 5, 6, 2, 5, 6. Мода равна пяти, т.к. число 5 встречалось наиболее часто. Другой пример. Имеются данные о размере обуви 11 девочек: 5, 3, 4, 3, 5, 4, 3, 4, 2, 6, 2. Поскольку наибольшую частоту имеют два соседних размера обуви 3 и 4, то модальное значение будет равно 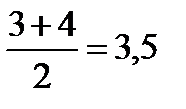 .
.
Модальным интервалом называется интервал, которому соответствует наибольшая частота. Для интервального ряда с равными интервалами, мода определяется по формуле:
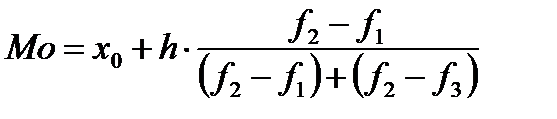 , (2.4)
, (2.4)
где 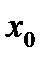 - начальная граница модального интервала;
- начальная граница модального интервала;
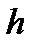 – величина модального интервала;
– величина модального интервала;

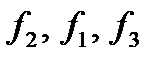 - частота модального интервала, частота интервала, предшествующего модальному, и частота интервала, следующего за модальным, соответственно.
- частота модального интервала, частота интервала, предшествующего модальному, и частота интервала, следующего за модальным, соответственно.
Пример 2.5. Определить моду ряда распределения роста группы девочек:
|
Медианойраспределения называется такое значение величины признака, которое делит упорядоченную последовательность его значений на две равные по численности части; причем у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – выше этого значения. Медиана дискретного ряда распределения в случае нечетного числа членов 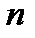 соответствует
соответствует 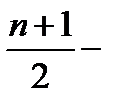 му значению ряда, а в случае четного числа членов
му значению ряда, а в случае четного числа членов 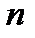 медиана равна среднему арифметическому
медиана равна среднему арифметическому 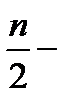 го и
го и 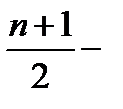 го значений ряда распределения. В случае интервального ряда распределения сначала определяют медианный интервал, т.е. такой интервал, в котором сумма накопленных частот превышает половину общего числа наблюдений, а затем численное значение медианы определяется по формуле:
го значений ряда распределения. В случае интервального ряда распределения сначала определяют медианный интервал, т.е. такой интервал, в котором сумма накопленных частот превышает половину общего числа наблюдений, а затем численное значение медианы определяется по формуле:
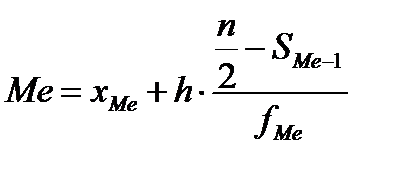 ,(2.5)
,(2.5)
где 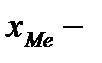 нижняя граница медианного интервала,
нижняя граница медианного интервала,
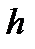 – величина медианного интервала,
– величина медианного интервала,
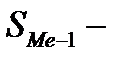 накопленная частота интервала, предшествующего медианному,
накопленная частота интервала, предшествующего медианному,
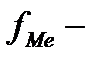 частота медианного интервала.
частота медианного интервала.
Пример 2.6. Найдем медиану ряда распределения роста девочек по данным таблицы из примера 2.5. Здесь медианный интервал 164 < 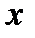 < 168. Поэтому имеем: < 168. Поэтому имеем:
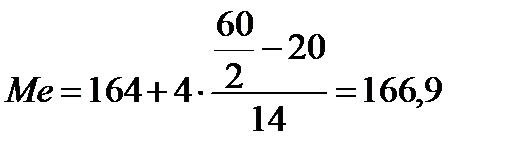 . .
|
Степенные средние.
К степенным средним относятся: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и др. Общая формула степенной средней имеет следующий вид:
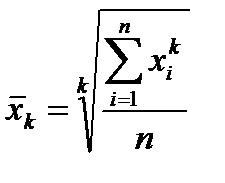 , (2.6)
, (2.6)
 где
где 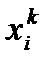 - варианта усредняемого признака,
- варианта усредняемого признака,
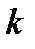 – показатель степени,
– показатель степени,
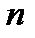 – число вариант (или объём выборки).
– число вариант (или объём выборки).
При 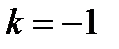 получается средняя гармоническая величина:
получается средняя гармоническая величина:
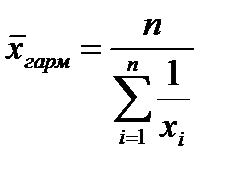 . (2.7)
. (2.7)
Если 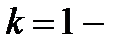 получаем среднюю арифметическую величину, при
получаем среднюю арифметическую величину, при 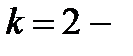 среднюю квадратическую и т.д.
среднюю квадратическую и т.д.
Средняя геометрическая величина – это предел при 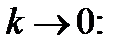
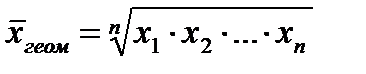 (2.8)
(2.8)
Пример 2.7.Найдем средние величины размера обуви пяти человек
|
Выполняются следующие неравенства:
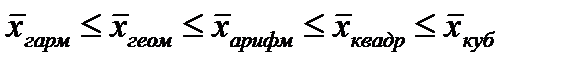
Дата добавления: 2016-06-02; просмотров: 797;

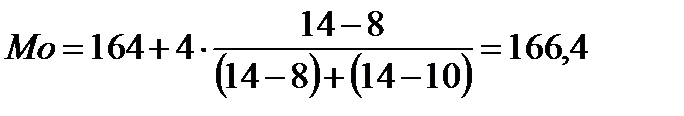 .
.