Относительные величины.
Относительные величины используют, если необходимо сопоставить явления, исследовать закономерности их изменения и развития, изучить структуру совокупностей. Относительная величина (ОВ)в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Величина, с которой сравнивают, называется базой (основанием) сравнения. ОВ выражаются в коэффициентах, если основание принимается за 1, в процентах, если основание принимается за 100, в промилле, если основание принимается за 1000, в продецимилле, если основание принимается за 10000.
Примеры относительных величин:
1. Относительная величина динамики (ОВД)– это результат сопоставления уровней одного и того же явления, относящихся к различным периодам или моментам времени. Различают относительные показатели динамики с постоянной и переменной базой сравнения. При изучении динамики за ряд периодов относительные показатели (или темпы роста), исчисленные по отношению к одной постоянной базе сравнения, называются базисными, а исчисленные по отношению к переменной
базе сравнения – цепными. Относительная величина динамики может быть представлена в виде коэффициента (индекса) роста (в долях), темпа роста (в процентах) и темпа прироста (темп роста минус 100%).
Пример 2.1. По данным Росстата величина прожиточного минимума в 2004 г. составила 2376 рублей в месяц в среднем на душу населения. В 2008 г. аналогичный показатель был равен 4593 рубля. Относительная величина динамики 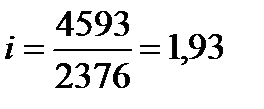 , т.е. величина прожиточного минимума в 2008 г. составляла 193% от уровня 2004 г. Показатель 1,93 принято называть коэффициентом роста, или индексом роста. Показатель 193% - это величина темпа роста, а величина , т.е. величина прожиточного минимума в 2008 г. составляла 193% от уровня 2004 г. Показатель 1,93 принято называть коэффициентом роста, или индексом роста. Показатель 193% - это величина темпа роста, а величина 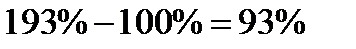 называется темпом прироста. В данном случае за 4 года величина прожиточного минимума выросла на 93%. называется темпом прироста. В данном случае за 4 года величина прожиточного минимума выросла на 93%.
|
2. Относительная величина структуры (ОВСт)характеризует доли, удельные веса составных элементов в общем итоге и выражается в долях, а чаще в процентах:
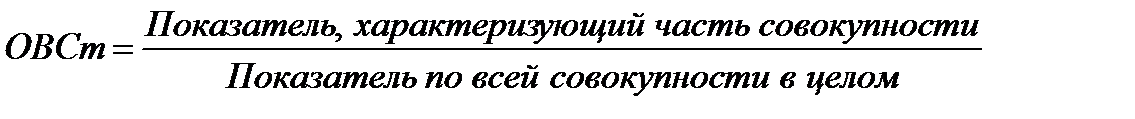 ,
,
т.е. 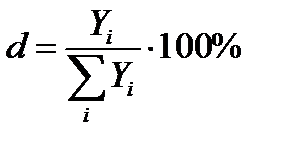 (2.1)
(2.1)
Пример 2.2.
Рассчитанные в последней графе этой таблицы проценты представляют собой относительные величины (удельные веса) структуры. |
3. Относительная величина сравнения (ОВС)сопоставляет размеры одноименных абсолютных величин, относящихся к одному и тому же периоду или моменту времени, но к различным объектам или территориям:
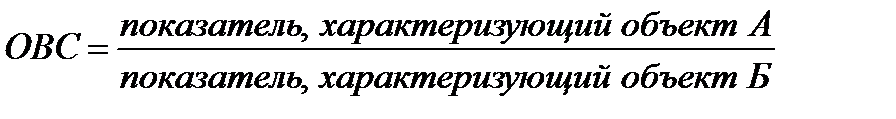 . (2.2)
. (2.2)
Например, по добыче газа в 2009 г. США опережали Россию в 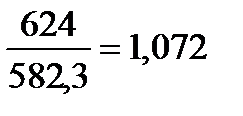 раза, т.е. уровень добычи газа в РФ составлял
раза, т.е. уровень добычи газа в РФ составлял 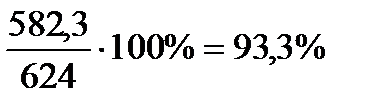 от уровня США.
от уровня США.
4. Относительная величина интенсивности (ОВИ)характеризует степень распространения или развития изучаемого процесса или явления:
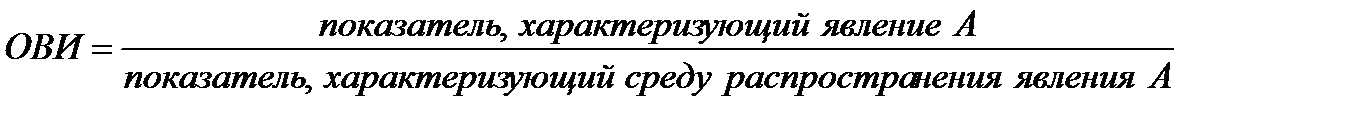 . (2.3)
. (2.3)
ОВИ получается сопоставлением разноименных, но взаимосвязанных в своём развитии величин, поэтому он представляет собой, как правило, именованную величину, но может быть выражен и в процентах.
Пример 2.3. При изучении демографических процессов рассчитываются показатели рождаемости 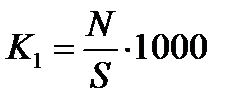 , смертности , смертности 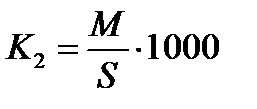 , естественного прироста , естественного прироста 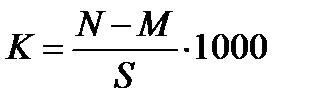 , т.е. как отношение числа родившихся , т.е. как отношение числа родившихся 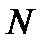 и умерших и умерших 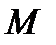 или величины прироста населения или величины прироста населения 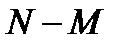 за год к среднегодовой численности населения за год к среднегодовой численности населения 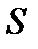 данной территории в расчете на 1000 человек. Так, по состоянию на 2008 г. в России данной территории в расчете на 1000 человек. Так, по состоянию на 2008 г. в России 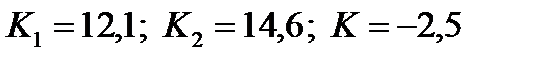 . .
|
Разновидностью ОВИ является относительная величина экономического развития, характеризующая производство продукции в расчете на душу населения и играющая важную роль в оценке развития экономики государства. При расчете этого показателя используют среднюю за период численность населения (например, среднегодовую).
| Пример 2.4. По данным МВФ по объему ВВП РФ в 2010 г. находится на 6 месте в мире – 2218,764 млрд. долларов США, что составляет 15,17 % от уровня ВВП США. Для того чтобы сделать вывод об уровне развития экономики, необходимо сопоставить её со среднегодовой численностью населения страны. В результате размер ВВП на душу населения составит 15806,877 долларов, что в 3 раза меньше, чем в США, и в 5,6 раза меньше, чем в находящемся по этому показателю на первом месте - Катаре. По уровню этого показателя РФ в 2010 году находится на 51 месте в мире. |
Средние величины.
Средняя величина (СВ) – это показатель, характеризующий типичный уровень явления и выражающий величину признака, отнесенную к элементу совокупности. Их делят на два класса:
• структурные средние (мода и медиана);
• степенные средние (средняя арифметическая, средняя геометрическая и др.).
Дата добавления: 2016-06-02; просмотров: 939;
