Закон Био-Савара-Лапласа.
Закон БСЛ позволяет вычислить индукцию поля в произвольной точке, которая создается проводников с током I.
Элемент проводника длиной 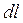 и сечением
и сечением 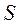 содержит
содержит 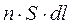 носителей тока (
носителей тока ( 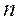 - концентрация носителей). Каждый из носителей создает поле с индукцией
- концентрация носителей). Каждый из носителей создает поле с индукцией
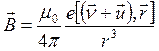 (18.6)
(18.6)
Среднее по всем носителям тока в элементе 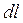 значение индукции
значение индукции
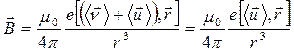 (18.7)
(18.7)
Умножив (18.7) на количество носителей тока в 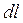 , получим индукцию, создаваемую элементом
, получим индукцию, создаваемую элементом 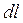 :
:
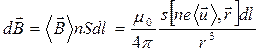 (18.8)
(18.8)
Поскольку 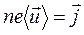 , выражение (18.8) принимает вид:
, выражение (18.8) принимает вид:
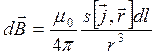 . (18.9)
. (18.9)
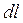 можно рассматривать как вектор, направленный вдоль
можно рассматривать как вектор, направленный вдоль 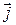 , и считать
, и считать
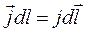 (18.10)
(18.10)
Соответственно получаем:
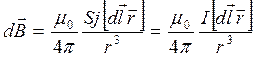 (18.11)
(18.11)
Соотношение (18.11) называется законом Био-Савара-Лапласа.
Вычисление индукции поля прямого тока
Индукция поля прямого тока находится по формуле 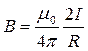 . Вывод этой формулы на основе закона Био-Савара-Лапласа изучить самостоятельно: § 42.
. Вывод этой формулы на основе закона Био-Савара-Лапласа изучить самостоятельно: § 42.
Сила Лоренца
На движущийся в магнитном поле заряд действует сила, которую естественно называть магнитной. Логично предположить, что эта сила должна быть пропорциональна величине заряда q , его скорости 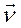 и индукции магнитного поля
и индукции магнитного поля 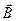 . Действительно, экспериментально установлено, что
. Действительно, экспериментально установлено, что
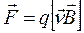 (18.12)
(18.12)
Отметим, что, в соответствии с определением, магнитная сила всегда перпендикулярна скорости заряда и индукции поля, а значит - работы над зарядом не совершает. (18.А = 0)
Если на заряженную частицу одновременно действуют электрическое и магнитное поля, то результирующая сила будет равна
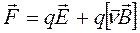 (18.13)
(18.13)
Эта сила называется силой Лоренца.
Закон Ампера
Закон Ампера определяет силу, действующую на проводник с током в магнитном поле. Получим формулу закона Ампера, исходя из выражения для силы Лоренца.
На каждый из носителей тока в проводнике, находящемся в магнитном поле действует сила
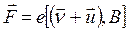 (18.14)
(18.14)
За счет взаимодействия носителей тока с остальным веществом проводника эта сила передается всему проводнику в целом. Усредняя силу (18.14) по всем носителям тока находящимся в элементе 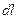 проводника, получаем:
проводника, получаем:
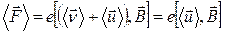 (18.15)
(18.15)
Число носителей тока в элементе 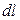 равно, очевидно,
равно, очевидно, 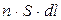 . Умножив, (18.15) на это число, получим
. Умножив, (18.15) на это число, получим
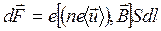 (18.16)
(18.16)
Учтем, что 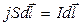 , а
, а 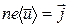 . Тогда (18.16) приводится к виду:
. Тогда (18.16) приводится к виду:
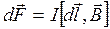 (18.17)
(18.17)
Формула (18.17) определяет силу, действующую на элемент тока 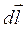 в магнитном поле, и выражает закон Ампера.
в магнитном поле, и выражает закон Ампера.
Дата добавления: 2016-06-02; просмотров: 650;
