III. Равносильности, выражающие основные законы алгебры логики.
1. 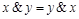 .
.
2. 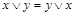 .
.
3. 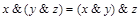 .
.
4. 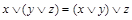 .
.
5. 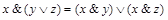 .
.
6. 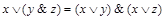 .
.
Доказать указанные равносильности (как и любой закон алгебры логики) можно: 1) построив таблицу истинности для правой и левой частей равенства; 2) с помощью диаграмм Эйлера – Венна; 3) путем правильных логических рассуждений.
Используя равносильности групп I, II, III, можно часть формулы алгебры логики или всю формулу заменить равносильной ей формулой. Равносильные преобразования формул применяются для доказательства равносильностей, для приведения формул к заданному виду, для упрощения формул.
Пример 4. Доказать равносильность 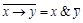 .
.
Решение: 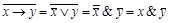 .
.
Пример 5. Упростить формулу 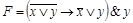 .
.
Решение: 
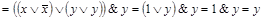 .
.
Пример 6. Доказать, что формула 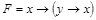 тождественно истинная.
тождественно истинная.
Решение:
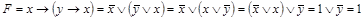 .
.
Всякая формула алгебры логики есть функция алгебры логики. Тождественно истинная и тождественно ложная формулы есть постоянные функции.
Определение: Функцией, двойственной к функции 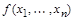 , называется функция
, называется функция
 .
.
Функция, двойственная самой себе, называется самодвойственной 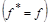 .
.
Теорема (связь таблиц функций 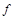 и
и 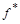 ): Таблица функции
): Таблица функции 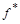 получается из таблицы функции
получается из таблицы функции 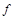 заменой всех нулей единицами, единиц – нулями и обозначения
заменой всех нулей единицами, единиц – нулями и обозначения 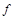 в заголовке на
в заголовке на 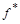 .
.
Следствие:
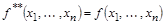 .
.
Таблица 4
Некоторые двойственные функции
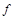
| 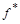
| |

| 
| |
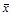
| 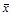
| |
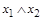
| 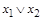
| |
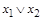
| 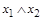
| |
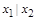
| 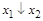
| |
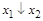
| 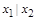
| |
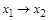
| 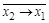
| |
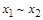
| 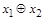
| |
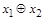
| 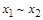
|
Докажем соотношения 1, 3, 4, 5, 7, 9, 10 из табл. 4:
1) 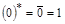 ;
;
3) 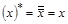 ;
;
4) 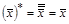 ;
;
5) 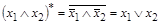 ;
;
7) 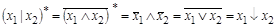 ;
;
9) 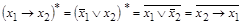 ;
;
10) 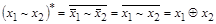 .
.
Соотношения 2, 6, 8, 11 следуют из доказанных в силу следствия последней теоремы. Из соотношений 3, 4 табл. 4 следует, что тождественная функция и отрицание самодвойственны.
Принцип двойственности: Пусть 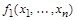 , … ,
, … , 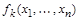 и
и 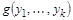 - булевы функции, и пусть
- булевы функции, и пусть
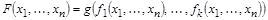
– сложная булева функция. Тогда
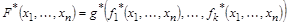 ,
,
то есть для получения двойственной к сложной функции 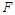 нужно все функции, входящие в
нужно все функции, входящие в 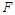 , заменить на двойственные.
, заменить на двойственные.
Таким образом, если функции равны, то и двойственные им функции равны. С помощью принципа двойственности можно получать новые эквива-лентные соотношения, переходя от равенства 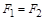 к равенству
к равенству 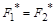 .
.
Пример 7. Докажем, что из свойства поглощения  следует равенство
следует равенство 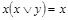 .
.
Решение: Пусть 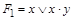 ,
, 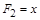 . Тогда по определению двойственной функции
. Тогда по определению двойственной функции 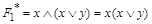 . Равенство
. Равенство 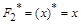 доказано ранее (см. табл. 4). Используя импликацию – если
доказано ранее (см. табл. 4). Используя импликацию – если 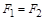 , то
, то 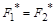 , получаем результат. Однако в данном примере принцип двойственности можно применить непосредственно:
, получаем результат. Однако в данном примере принцип двойственности можно применить непосредственно:
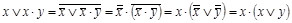 .
.
Пример 8. Показать, что формула 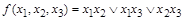 задает самодвойственную функцию.
задает самодвойственную функцию.
Решение: Таблица истинности для данной формулы показана в примере 1 (с. 5). Из этой таблицы получаем 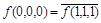 ,
, 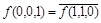 ,
, 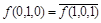 ,
, 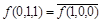 .
.
Дата добавления: 2016-05-25; просмотров: 1919;
