Эквивалентность формул. Принцип двойственности

При исследовании логических формул во многих случаях требуются их корректные преобразования, позволяющие получить новые формулы, эквивалентные данным. Корректность преобразований обеспечивается выполнением следующих правил.

Правило подстановки формулы 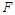вместо переменной : все вхождения переменной в исходное соотношение должны быть одновременно заменены формулой .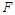

Правило замены подформул: если какая-либо формула 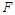, реализующая функцию 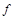, содержит 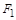в качестве подформулы, то замена 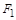на эквивалентную 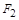не изменит функцию .

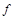Эти два правила называются эквивалентными преобразованиями, так как в результате их применения получаются формулы, эквивалентные исходным.

На основании этих правил в алгебре логики действует принцип суперпозиции: любая сложная функция может быть представлена в виде совокупности элементарных функций двух аргументов. Например,

.

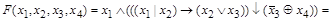
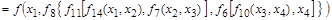Упражнение (выполнить самостоятельно): Составлением таблицы истинности проверить соотношени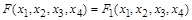е: , где .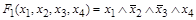

Формулы, представляющие одну и ту же функцию, называются эквивалентными или равносильными.

Отношение равносильности рефлексивно, симметрично и транзитивно.

Пример 3. Доказать эквивалентность формул стрелки Пирса путем восстановления таблицы значений функции.

Решение: Составим таблицу:

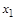
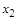
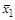
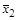
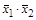
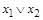
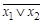
Из сопоставления пятого и седьмого столбцов таблицы следует результат.

Формула 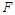называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных. Например, тождественно истинны формулы: , .

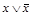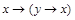Формула 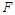называется тождественно ложной, если она принимает значение 0 при всех значениях входящих в нее переменных. Например, тождественно ложна формула: .

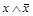Между понятиями равносильности и эквивалентности ( 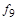в табл. 2) существует следующая связь: если формулы 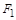и 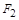равносильны, то формула 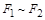– тавтология, и обратно, если формула 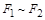– тавтология, то формулы 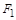и 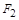равносильны.

Важнейшие равносильности можно разбить на три группы: