Высказывания и логические операции над ними

Таблица 1

Булевы функции одной переменной

	0 1	Обозначение	Наименование
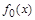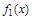
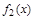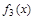
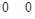
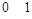
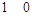
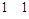
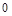
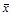
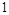
			Константа 0 Тождественная Отрицание Константа 1

Функци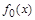и и 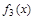- константы, равные 0 и 1 соответственно, следовательно, их значения не зависят от значений переменной, она – фиктивна. Функция 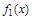- тождественная, повторяет , то есть 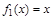. Функция 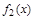называется отрицанием и обозначается 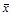. Ее значение противоположно значению , то есть 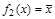. Таким образом, описаны все унарные операции на множестве .

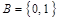Рассмотрим бинарные операции на этом множестве, реализовываемые булевыми функциями двух переменных (табл. 2).

Таблица 2

Булевы функции двух переменных

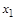
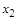
	0 0 1 1 0 1 0 1	Обозначение	Наименование
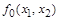
	0 0 0 0		Константа 0
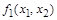
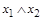
	0 0 0 1		Конъюнкция
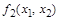
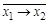
	0 0 1 0		Запрет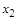
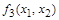
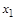
	0 0 1 1		Повтор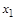
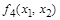
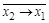
	0 1 0 0		Запрет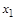
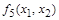
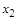
	0 1 0 1		Повтор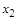
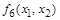
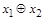
	0 1 1 0		Сложение по mod 2
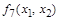
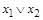
	0 1 1 1		Дизъюнкция
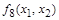
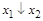
	1 0 0 0		Стрелка Пирса
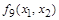
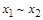
	1 0 0 1		Эквивалентность
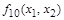
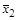
	1 0 1 0		Отрицание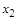
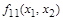
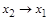
	1 0 1 1		Правая импликация
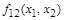
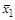
	1 1 0 0		Отрицание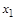
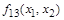
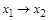
	1 1 0 1		Левая импликация
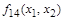
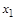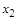
	1 1 1 0	|	Штрих Шеффера
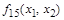
	1 1 1 1		Константа 1

Некоторые функции табл. 2 имеют несколько обозначений и наименований. Обратим внимание только на следующие из них.

Конъюнкция (логическое "и") 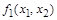называется также логическим умножением и обозначается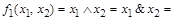

.

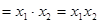Дизъюнкция (соединительное "или") 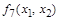называется логическим сложением и обозначается .

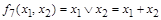Функция 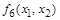- это сложение по модулю 2 (исключающее "или", дизъюнкция с исключением). Ее обозначения: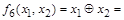

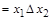. Она равна 1, когда значения ее аргументов различны, и равна 0, когда они равны. Поэтому функцию 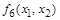иногда называют неравнозначностью.

Функция 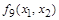называется эквивалентностью (эквиваленцией) или равнозначностью. Ее обозначения: .

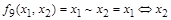Функция 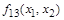называется импликацией (левой импликацией). Ее обозначения: .

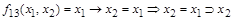Стрелка Пирса (табл. 2) называется также функцией Вебба, а штрих Шеффера – функцией Шеффера.

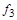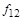В функциях и переменная 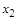- фиктивна, а именно: 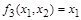, 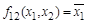. Аналогично у функци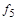й и 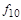фиктивна переменная 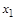: 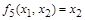, 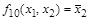. Таким образом, из 16 функций двух переменных (табл. 2) шесть функций ( 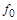, , 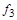, , 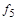, 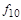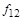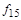) имеют фиктивные переменные. С ростом числа переменных 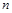доля функций, имеющих фиктивные переменные, убывает и стремится к нулю.

Для решения некоторых задач булевы функции (табл. 2) целесообразно представлять в виде таблицы 3, из которой следует, что каждой функции соответствует ее отрицание (например, константа 1 – отрицание константы 0). Данное свойство используется в принципе двойственности алгебры логики (см. п. 4). В качестве полного набора функций, которым соответствуют их отрицания, можно указать (табл. 3) восемь: 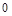, , 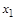, , 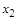, , 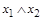, 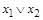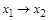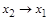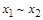. При формировании этого (или подобного) набора используется совокупность следующих понятий: логические константы, логические переменные, отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность. Эта совокупность часто используется при решении содержательных логических задач, где с помощью данных понятий исследуются отношения между высказываниями. Следующий параграф посвящен описанию элементарных логических операций над высказываниями.

Высказывания и логические операции над ними

Понятие высказывания является основным неопре­деляемым понятием математической логики. Под выс­казыванием понимают любое повествовательное предло­жение, о котором можно сказать, истинно оно или ложно в данных условиях места и времени. Логическое значе­ние высказывания «истина» («ложь») обозначается или буквой и (л), или цифрой 1, (0).

Таблица 3

Булевы функции двух переменных

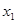
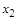
	0 0 1 1 0 1 0 1	Обозначение	Наименование
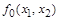
	0 0 0 0		Константа 0
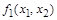
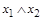
	0 0 0 1		Конъюнкция
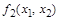
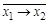
	0 0 1 0		Отрицание левой импликации
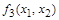
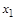
	0 0 1 1		Переменная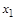
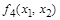
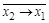
	0 1 0 0		Отрицание правой импликации
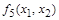
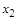
	0 1 0 1		Переменная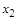
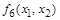
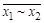
	0 1 1 0		Отрицание эквивалентности
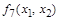
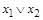
	0 1 1 1		Дизъюнкция
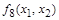
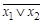
	1 0 0 0		Отрицание дизъюнкции
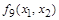
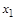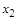
	1 0 0 1	~	Эквивалентность
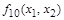
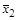
	1 0 1 0		Отрицание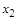
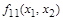
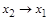
	1 0 1 1		Правая импликация
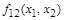
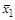
	1 1 0 0		Отрицание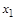
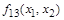
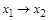
	1 1 0 1		Левая импликация
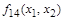
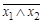
	1 1 1 0		Отрицание конъюнкции
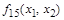
	1 1 1 1		Отрицание константы 0

В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Отрицанием высказывания называется высказы­вание 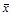, которое истинно, если ложно, и ложно, если истинно. Высказывание 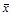читается так: "не " или "неверно, что ".

Конъюнкцией высказываний 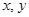называется выска­зывание 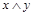, которое истинно, если и 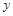истин­ны, и ложно, если хотя бы одно из них ложно. Высказы­вание 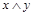читается: " и ".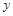

Дизъюнкцией высказываний 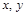называется выска­зывание 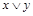, которое истинно, если хотя бы одно из высказываний или 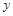истинно, и ложно, если оба они ложны. Читается: " или ".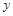

Импликацией высказываний 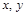называется выска­зывание 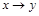, которое ложно, если истинно и 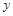лож­но, и истинно во всех остальных случаях. Читается: "если , то 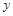" или "из следует ".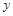

Эквивалентностью высказы­ваний 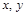называется высказывание 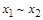, которое ис­тинно, если оба высказывания и 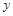одновременно ис­тинны или ложны, и ложно во всех остальных случаях. Читается: " тогда и только тогда, когда 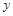" или "для того чтобы , необходимо и достаточно, чтобы ".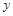

Пример 2. Среди следующих предложений выделить высказывания, установить, истинны они или ложны:

1) Москва – столица России;

2) все студенты любят математику;

3) некоторые студенты любят математику;

4) пейте молоко!;

5) который час?;

6) ;

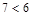7) ;

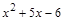8) ;

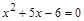9) ;

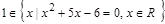10) это предложение ложно;

11) целое число делится на 5 тогда и только тогда, когда оно заканчивается на 0 или на 5;

12) если число делится на 10, то оно делится на 5;

13) если коровы летают, то 2 + 2 = 5.

Решение: Высказывания 1), 3), 9), 11), 12), 13) – истинные; высказывания 2), 6) – ложные; предложения 4), 5), 7), 8), 10) не являются высказываниями. Предложение 11) является истинной эквивалентностью. Предложения 12), 13) являются истинными импликациями.

Подробнее разберем предложение 13). Высказывание "коровы летают" = 0 – ложное, высказывание " 2 + 2 = 5 " = 0 – ложное. Тогда на основании таблицы истинности для импликации (табл. 2) значение высказывания: 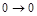равно 1, то есть высказывание 13) истинно.

Все высказывания можно разделить на простые (или элементарные) и составные (или сложные).

Любое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения определенных выше логических опера­ций, называется формулой алгебры логики.