Вероятность отклонения относительной частоты от постоянной
Вероятности в независимых испытаниях.
Обозначим через 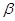 вероятность того, что относительная частота “успехов” в n испытаниях Бернулли отклонится от вероятности “успеха” p не более , чем на
вероятность того, что относительная частота “успехов” в n испытаниях Бернулли отклонится от вероятности “успеха” p не более , чем на 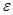 >0. Имеем
>0. Имеем
P(½ 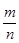 - p ½
- p ½ 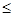
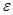 ) =
) = 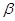 .
.
Если n достаточно велико, то величина 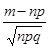 имеет стандартное нормальное распределение N(0,1). Воспользуемся формулой Муавра – Лапласа
имеет стандартное нормальное распределение N(0,1). Воспользуемся формулой Муавра – Лапласа
P( 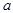
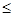
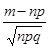
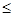
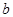 ) » F(
) » F( 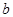 ) – F(
) – F( 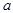 ) и запишем
) и запишем
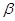 =P( –
=P( – 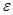 n
n 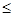
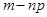
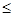
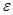 n ) = P( –
n ) = P( – 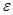
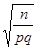
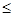
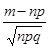
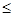
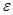
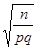 ) »
) »
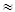 F(
F( 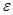
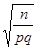 ) – F(-
) – F(- 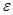
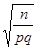 )= 2F(
)= 2F( 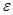
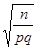 ).
).
Это равенство содержит четыре параметра: n, p, 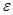 ,
, 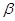 . Зная три из них, можно найти четвертый. Пусть, например, известны p,
. Зная три из них, можно найти четвертый. Пусть, например, известны p, 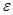 и
и 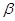 . Определим n, воспользовавшись выведенной формулой F(
. Определим n, воспользовавшись выведенной формулой F( 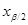 ) =
) = 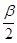 , где
, где 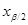 =
= 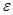
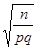 – квантиль нормального распределения, отвечающая уровню вероятности
– квантиль нормального распределения, отвечающая уровню вероятности 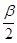 . Так как F(
. Так как F( 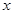 ) монотонно возрастающая функция, то
) монотонно возрастающая функция, то 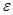
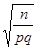
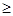
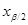 , откуда
, откуда
n 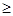 pq
pq 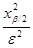 . Если p неизвестно, то воспользуемся тем, что pq
. Если p неизвестно, то воспользуемся тем, что pq 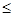
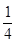 . Тогда
. Тогда
n 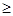
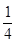
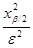 .
.
Пример. Для определения доли избирателей, поддерживающих кандидата A, производится выборочное обследование. Определить объем выборки, при которой с вероятностью, не меньшей 0,99, погрешность составит менее 0,05.
Решение. По условию задачи 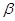 = 0,99 ,
= 0,99 , 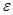 = 0,05. Вероятность p неизвестна. Воспользуемся формулой n
= 0,05. Вероятность p неизвестна. Воспользуемся формулой n 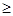
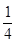
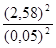 = 665,64 » 666.
= 665,64 » 666.
Дата добавления: 2016-06-24; просмотров: 1217;
