Закон больших чисел.

В теории вероятностей и ее приложениях часто рассматриваются случайные величины, являющиеся, в свою очередь суммами большого числа случайных величин. Непосредственное вычисление распределения вероятностей суммы большого числа случайных величин обычно связано с большими трудностями. 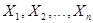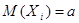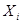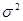В то же время известно, что среднее арифметическое независимых одинаково распределенных случайных величин , имеющих и D( )= при больших n ведет себя устойчиво, имеет малое рассеяние относительно a, его дисперсия стремится к нулю при n 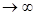. Таким образом, при больших значениях n можно в определенном смысле считать, что среднее арифметическое n независимых случайных величин приближенно равно числу a, т.е. практически не зависит от случая.

Математическую формулировку свойства устойчивости среднего арифметического n случайных величин дают теоремы, известные какзакон большихчисел(з.б.ч.).

Разные теоремы закона больших чисел отличаются исходными вероятностными моделями и различными формами статистической устойчивости. Исторически первой формой з.б.ч. была теорема Я.Бернулли (опубликована в
1713 г.) об устойчивости относительной частоты в модели повторных независимых испытаний. Затем она была обобщена Хинчиным А.Я. на случай испытаний с изменяющейся вероятностью 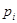, где i – номер испытания. Значительно более общие формы закона больших чисел были доказаны П.Л.Чебышевым (1811–1894 г.г.), А.А. Марковым (1856–1922 г.г.) и др.